JAGSでWAICを計算するためのメモ
試しに計算してみたのですが,まだ細部を理解できていないので,検証用にメモを残しておきます.
豊田本2017(『実践ベイズモデリング』)にStanからWAICを計算する手順が解説されていたので,それを参考にして
JAGSから作ったサンプルでWAICを計算してみます.
例によってJAGSをRから呼び出すのにパピー4匹本のDBDA2E-utilities.Rを使います.
まずJAGS用のmodel{ }内に
# Generated quantities for (i in 1:N) { loglikelihood[i] <- log(dnorm(y[i], mu[i], 1/ (s * s))); }
などを追加して,推定したパラメータとデータを用いた対数尤度を計算します.
この場合はパラメータはmuとsです.muは説明変数に回帰しているので添え字[i]がついています.
確率密度関数は応答関数にあわせて適宜修正しましょう.
coda.samplesの結果を格納します.
mcmcCoda = coda.samples( jagsModel , variable.names=parameters , n.iter=nPerChain , thin=thinSteps )
ここから対数尤度を整形して取り出し,looパッケージのwaic関数に渡します.
こちらの記事を参考にさせていただきました.
library(loo) loglik1 <- sapply(1:N, function(i) unlist(mcmcCoda[, paste("loglikelihood[", i, "]", sep = "")])) waic(loglik1)
これでStanから計算した結果とほぼ同じWAICが出力されました.
looパッケージのextract_log_lik関数を使えばもっと簡潔になりそう.
TikZ
TikZで簡単かつ綺麗な図がかけるので,これがあれば研究の分析・報告・文章化は全てTeX+beamerだけで事足りるでしょう.
使わないとすぐに忘れそうなので,ポイントだけメモしておきます.
簡易マニュアルでも推奨しているように,最初にグリッドを書いておくと作業が大変ラクです.
これは
\draw[step=1,black!10, very thin] (0,0) grid (12, 8 );
などと入力するだけでOKです.デフォルトの座標単位が1cmなので紙の大きさに合わせて,調整すればよいでしょう.
あとはnodeで数式やプレースフォルダを配置して,drawで矢印を足していく感じ.
nodeの座標は始点位置を指定できるので,例えば
\node [right] at (0.5,7.5 )
のように書いて,調整します.基本的に[right]でいいでしょう.ただしオブジェクトを丸で囲む場合は,サークルの中心点とラベル(ノード)の中心点を合わせましょう.
矢印は
\draw[thick,-latex] (7.5 ,3 ) -- (9.5 ,2.2 ); \draw[thick,-latex] (7.5 ,1 ) -- (9.5 ,1.8 );
こんな感じで始点と終点を指定します.
狙った位置にオブジェクトをビシッと配置できるので気持ちがいいです.

まあ,パワポとどっちがラクやねんと言われれば,パワポのほうが手っ取り早い気もしますが,数式の美しさと再現可能性を考慮すればbeamer + TikZがオススメです.
Texworks ショートカットキーのカスタマイズ
Texworksのショートカットキーの設定を編集すると,任意のTeXコマンド入力を登録できます.
例えばTeXソース編集中に
図 + tab
と入力するだけで,
\begin{figure}[h] \begin{center} \includegraphics[scale=0.5]{ .pdf} \caption{•} \label{american} \end{center} \end{figure}
というコマンドが挿入できます.
つまり自分が選んだ好きな文字の後にtabキーを押すだけで,
任意のコマンドを挿入できるように設定できます.
これは簡単かつ便利な機能なので是非使ってください.
よく使うコマンドの大半はデフォルトの設定で用意されています.
たとえばギリシア文字の場合
xa+tab
で
\alpha
に変換されます.
設定の方法
まず
\texmf-config\texworks\completion
フォルダ内の
tw-latex.txt
を開きます.
例えば
bite+tab
という入力に対して
\begin{itemize} \item \item \end{itemize}
というコマンドの入力を対応させるには,
tw-latex.txtの中に
bite:=\begin{itemize}#RET# \item #INS# #RET# \item #RET# #RET#\end{itemize}
という一文を追加するだけでOKです.
#RET#は改行で,#INS#は入力後のカーソル位置です.•を入れておけば,tabでその場所に飛びます.環境内で順番に入力するスペースが決まっている場合はあらかじめ
•をいれておくと便利です.
私がよく使っているキーはこんな感じです
v:=\verb|#INS#| v:=\verb|#INS#| (:=\left( #INS# \right) {:=\left{ #INS# \right} (:=\left( #INS# \right) {:=\left{ #INS# \right} 図:=\begin{figure}[h]#RET# \begin{center} #RET# \includegraphics[scale=0.5]{#INS#.pdf}#RET# \caption{•} #RET# \label{american} #RET# \end{center}#RET#\end{figure} 表:=\begin{table}[h]#RET# \caption{}\label{}#RET# \begin{center} #RET# \begin{tabular}{ccc}#RET# #INS# & & \\ #RET# & & \\ #RET# & & \\ #RET# \end{tabular} #RET# \end{center} #RET# \end{table} 定義:=\begin{definition}[] #INS# #RET#\end{definition} 命題:=\begin{prop} #INS# #RET#\end{prop} 定理:=\begin{} #INS# #RET#\end{} 系:=\begin{} #INS# #RET#\end{} 行列:=\begin{pmatrix}#RET# & \\#RET# & \\ #RET#\end{pmatrix} bite:=\begin{itemize}#RET# \item #INS# #RET# \item #RET# #RET#\end{itemize} ni:=\begin{nitem}#RET# \item #INS# #RET# \item #RET# #RET#\end{nitem} e:=\begin{align*}#RET# #INS# & = \\ #RET# & = #RET#\end{align*} f:=\frac{#INS#}{•} %nitem:=\begin{nitem}#RET# \item #INS# #RET# \item #RET#\end{nitem} r:=\sqrt{#INS#} s:=\sum_{#INS#}^{•} 4:=$$#INS# 4:=$$#INS#
全角文字でも使えるのがポイントです.日本語でTeXを入力している時,入力モードを切り替えるのが面倒ですよね.そんなとき
このショートカットを全角文字に割り当てておけば,いちいち切り替えなくも入力できます.
Income Segregation
この論文を読んでいて,Income Segregation と Race Segregation を組み合わせて表現するコードを思いついたので,メモを残しておきます.
以前から,シェリングのsegregation modelにエージェントの所得情報を別のレイヤーで表示させる,というアイデアを思いついていました.
ただ,面倒な割にインプリケーションも少ないかなと思って,今日まで実装するに至りませんでした.
しかし,Reardonのような実証論文があるということは,理論的な挙動を把握するためのプロトタイプを作ってみるのも悪くないかと思い,今回試しにやってみた次第です.
例によってコードはMathematicaでちゃちゃっと書きます*1.
所得情報のArrayPlot
まずエージェントの所得情報をArrayPlotするModuleを考えます.最初にエージェント毎に所得ベクトルを生成します.
(* income の初期情報を与える *) income[redn_, bluen_, mred_, mblue_] := Module[{sigma = 1}, {RandomVariate[LogNormalDistribution[mred, sigma], redn], RandomVariate[LogNormalDistribution[mblue, sigma], bluen]} ];
次に位置情報の初期配置を与えます.
(*赤agent 青agentの初期配置*) initialset[size_, redn_, bluen_] := Module[{a, b, n = redn + bluen}, Developer`ToPackedArray[(* Integer型指定で高速化 *) a = RandomSample[Range[size*size], n];(* 総エージェント数だけ1次元配列から非復元抽出 *) b = Flatten[Table[{i, j}, {i, 1, size}, {j, 1, size}], 1];(* 2次元座標 *) (* 抽出した1次元配列番号を座標に変換する. 前半は赤,後半は青用 *) {Table[b[[a[[i]]]], {i, 1, redn}], Table[b[[a[[i]]]], {i, redn + 1, n}]}, Integer] ]; (* 非復元抽出で初期配置を与える. output: {{赤の位置情報},{青の位置情報}} の順で出力する*)
これは以前に解説した関数と同じです.
次に所得情報を位置情報に対応させてArrayPlotするための関数を定義します.
(* 所得情報をplotする関数 *) visualize2[{redposi_, blueposi_}, incomelist_, size_] := Module[{zero1 = zerogrid[size], redincome, blueincome(* sizeは Manipulate内で指定*)}, (* Embedding agents into zero1 for visualization 引数のredposi_,blueposi_はそれぞれ「赤」と「青」の現在位置 *) redincome = incomelist[[1]]; blueincome = incomelist[[2]]; Do[zero1[[ Sequence @@ redposi[[i, {1, 2}]]]] = redincome[[i]], {i, Length[redposi]}]; Do[zero1[[ Sequence @@ blueposi[[i, {1, 2}]]]] = blueincome[[i]], {i, Length[blueposi]}]; ArrayPlot[zero1, ImageSize -> {300, 300}, AspectRatio -> Automatic, Frame -> False, Mesh -> All, Axes -> False] ];
ここではゼロのならんだグリッドに,エージェントの位置に応じて所得値を割り当てます.例えばもとの3次正方行列のゼログリッドが
0,0,0,
0,0,0,
0,0,0
だった場合に,3人分の所得{5,3,2}を位置情報{{1,3},{2,1},{3,3}}に割り当てると
0,0,5,
3,0,0,
0,0,2
という出力を得ます.後は所得の大小に応じてグレーに色分けしてプロットする必要があるのですが,ArrayPlotのデフォルト設定をそのまま利用します.
実はデフォルトで数字の大小に応じたグレースケールに変換して,Plotしてくれるのです(便利やー).
この部分,おもしろくない割に最初から作ると面倒なので,助かります *2
さて,ここで注意すべきは,次の点です.
- 位置情報の動的更新をせずに,所得値の情報だけ正しい位置に表示できるかを確認する.
- これができたら,動的更新のModuleに組み込む*3
次にパネルを二つ並べるために, GraphicsRowをManipulateのオブジェクトとして指定します.
GraphicsRow[{
ArrayPlot[{Table[Random[], {5}]}],
ArrayPlot[{Table[Random[], {5}]}]
}]
括弧の数に注意しましょう.できあがりはこんな感じです.
右のパネルが所得値を表しています.黒いほど高額所得です.
実行すると二つのパネルが同期して動きます.
人種に関する選好だけを持っていたとしても,人種間の所得分布に差があるとき,結果としてincome segregation(金持ちが金持ち同士で固まって住む)が生じる様子が分かります.これは統計的差別がもたらす意図せざる結果の一種と解釈することも可能です.
ただし,ここまでの結論は計算しなくてもほぼ自明なので,今後は
- 片方の人種だけに同人種への選好があっても,
income segregationが生じるのか? - 人種選好が
income segregationに及ぼす影響の推定 - 逆に人種選好はないが,incomeへの選好だけあるとき,人種間
segregationはどの程度生じるのか - 地価上昇ダイナミクスを取り入れると,人種間不平等がどのくらい高まるのか
などを考えてみようと思います.
*1:なお,自分で試してみたい学生は,授業で配布したサンプルコードをいきなり修正せず,追加すべきModuleだけプロトタイプを作り,実験してから組み込むようにしてください
*2:こういう内蔵関数が豊富なところが,Mathematicaのいいところだなあ
*3:はじめてシミュレーションに取り組む学生は,1ステップずつ作業を進めてください.複数のクロージャをまとめて更新すると,どこでエラーが出たか分かりません.慣れるまでは,1つずつエラーを直しながら進めてください.面倒なようですが,このほうが結果的に早いのです.さもなければバグがどこにあるか一日中探さなくてはなりません.はじめのうちはバグを直すより,バグを見つける方が難しいのです
研究会用メモ
案の定,2週間ほど前にやった計算をすっかり忘れて,同じコードを書くところであった. ブログにメモを残しておいたおかげで,思い出した.
というわけで
という実験の続きを再開する(10/11のエントリの続きです). 参照したコードは,例によって Kruschke氏のコードである.
準備はこれだけ
source("DBDA2E-utilities.R") fileNameRoot="Jags-lognormal-direct-sim" graphFileType="png"
まずR内で人工データを発生させる
# "t" means "true value" y0t=10; bt=0.1; pt=0.3; nt=25; mu=log(y0t)+nt*log(1-bt)+log((1+bt)/(1-bt))*nt*pt sigma= sqrt(nt*pt*(1-pt)*(log((1+bt)/(1-bt)))^2) gmc = rlnorm( n=500, mu, sigma)
pt, bt, nt が推定すべき真のパラメータである.
mu, sigmaがこのような決定論的関数で表される理由はgmcで証明が与えられる(ここ重要)
次にJAGSにわたすためのデータを定義する
dataList = list( y = gmc , N = length(gmc), nt=nt, y0t=y0t)#JAGSに渡すパラメータはlist内で再定義する # nt, y0tはR内で定義されているがJAGSにはdataを介して # 渡している.
nt,y0tはスカラである.dataListはRオブジェクトだが,modelstringで参照するために,このようなリストを作っておく
JAGSにわたすモデルを複数定義する.今回は
modelstring0
modelstring1
modelstring2
の三つ.
modelstring0 = " model{ for( i in 1 : N ) { y[i] ~ dlnorm(m, 1/(s^2))} m <- log(y0)+n*log(1-b)+log((1+b)/(1-b))*n*p s <- sqrt(n*p*(1-p)*(log((1+b)/(1-b)))^2) n ~ dpois(mean.n)#nをポアソン分布で近似 mean.n ~ dunif(1,2*nt) y0 ~ dpois(mean.y0)# mean.y0 ~ dunif(1,2*y0t) # y0t=10; bt=0.2; pt=0.65; nt=25; p ~ dbeta(1,1)#p,bの事前分布にβ分布 b ~ dbeta(1,1)}" # close quote for modelstring
modelstring0は推定するパラメタが一番多い.
つぎは,より理論モデルに忠実な設定.
#modelstring1は理論的に固定すべきパラメータn,y0を定数にする modelstring1 = " model{ for( i in 1 : N ) { y[i] ~ dlnorm(m, 1/(s^2)) } y0 <- y0t n <- nt m <- log(y0)+n*log(1-b)+log((1+b)/(1-b))*n*p s <- sqrt(n*p*(1-p)*(log((1+b)/(1-b)))^2) #prior for hyper parameters p ~ dbeta(1,1) b ~ dbeta(1,1) }" # close quote for modelstring
modelstring1はn,y0を定数として固定する.
ここで,先ほど定義したリスト内のスカラを割り当てる
(最初はRのグローバル変数を参照していたのだが,modelstringの中からは参照できないことが分かった.
まあ,よく考えればこっちはJAGSが読むコードなので,当然である )
最後のモデル.
# dilectly assign mean of poisson dist. of n,y0 modelstring2 = " model{ for( i in 1 : N ) { y[i] ~ dlnorm(m, 1/(s^2))} m <- log(y0)+n*log(1-b)+log((1+b)/(1-b))*n*p s <- sqrt(n*p*(1-p)*(log((1+b)/(1-b)))^2) n ~ dpois(nt)#nをポアソン分布で近似 y0 ~ dpois(y0t)# p ~ dbeta(1,1)#p,bの事前分布にβ分布 b ~ dbeta(1,1)}"
最後に,ハイパーパラメータだけ,真の値を代入してその他を推定するモデル
モデルの選択はこんな風にswitchで定義する.(文字型しかダメなのだろうか?)
a<-"1" modelstring<-switch(a, "0"=modelstring0, "1"=modelstring1, "2"=modelstring2)
モデルによって推定するパラメータは直に指定する
parameters0 = c("p","b","n","mean.n","mean.y0","y0","m","s") parameters1 = c("p","b","m","s") parameters2 = c("p","b","n","y0","m","s") parameters<-switch(a, "0"=parameters0, "1"=parameters1, "2"=parameters2)
あとは細かい話だが,plotPostに渡すパラメタがモデルによって異なるので, if文でモデル毎に指定しておく.
分析の度に,モデル選択変数aを指定することに注意する.
#全model共通で推定するパラメタ postInfo = plotPost( mcmcChain[,"p"] , xlab="success p" ) postInfo = plotPost( mcmcChain[,"b"] , xlab="interest b" ) #以下モデルに合わせてplotするパラメタを選択 if(a=="0") postInfo = plotPost( mcmcChain[,"n"] , xlab="time n" ) if(a=="0") postInfo = plotPost( mcmcChain[,"mean.n"] , xlab="mean of n" ) if(a=="0") postInfo = plotPost( mcmcChain[,"mean.y0"] , xlab="mean of y0" ) if(a=="1") postInfo = plotPost( mcmcChain[,"m"] , xlab="mu of y") if(a=="1") postInfo = plotPost( mcmcChain[,"s"] , xlab="sigma of y") if(a=="2") postInfo = plotPost( mcmcChain[,"n"] , xlab="time n" ) if(a=="2") postInfo = plotPost( mcmcChain[,"y0"] , xlab="y0" ) if(a=="2") postInfo = plotPost( mcmcChain[,"m"] , xlab="mu of y") if(a=="2") postInfo = plotPost( mcmcChain[,"s"] , xlab="sigma of y") saveGraph(file=fileNameRoot,type=graphFileType)
モデル1の推定結果

やはり理論的に固定すべき変数を真値で与えたデータの場合,未知のp,bの推定が
正確である.
問題はnt,y0tが現実のデータから推測できないことである.さてどうしよう...
■
Refreshに関するメモ
Mathematica内蔵関数Refreshの引数である,UpdateIntervalは更新を制御できたりできなかったりして,いまいち仕組みが分からない.そこでいろいろと実験してみた.
Manipulate[ Refresh[Random[], UpdateInterval -> If[go, 0.105, Infinity]], {{go, False}, {True, False}}]
このようなコードなら,UpdateIntervalによって更新頻度が制御できる.一方で
x = 1; Manipulate[ Refresh[x = x + 0.01; x, UpdateInterval -> If[go, 0.02, Infinity]], {{go, False}, {True, False}}]
これはUpdateIntervalがInfinityにもかかわらず暴走してしまう
そこでRefreshの中にIfを挟んで代入を制御する.
x = 1; Manipulate[ Refresh[ If[go, x = x + 0.01], UpdateInterval -> If[go, 1, Infinity]], {{go, False}, {True, False}}]
これならオンオフだけ制御できる.しかしインターバルの時間は指定通りにならない.
TrackedSymbols -> {} で制御しようとしてもうまくいかない.
結局,即時割り当てをManipulateの中に入れると,Dynamicに更新されるので,その場合はUpdateIntervalで制御できる範疇を超えてしまうらしい.
オブジェクトを再帰的代入すると,refreshしてもうまくいかないらしい
次のような命令なら代入でも問題ないし,UpdateIntervalによる制御もうまくいく
Manipulate[ Refresh[ If[go, x = Random[]], UpdateInterval -> If[go, 0.8, Infinity]], {{go, False}, {True, False}}, Button["reset", go = False; x = 100] ]
しかし再帰的に代入すると,Dynamicオブジェクトが自分自身を連続的に更新するので UpdateIntervalを指定しても,機能しない (のではないかと推測する)
Manipulate[ Refresh[ If[go, x = x + Random[]], UpdateInterval -> If[go, 0.8, Infinity]], {{go, False}, {True, False}}, Button["reset", go = False; x = 100] ]
グラフィックオブジェクトの動的更新
例えばつぎのようなDynamicオブジェクトはRefreshによって動的に更新される
(ただし止まらない)
Dynamic[Refresh[Histogram[RandomReal[10, 100]], UpdateInterval -> 0.1]]
制御したければManipulate内に入れて,チェックボックスでUpdateIntervalの値を指定する方法がある.
Manipulate[ Refresh[Histogram[RandomReal[10, 1000]], UpdateInterval -> If[x, 0, Infinity]], {{x, False}, {True, False}}]
今まで,ピコピコ系アウトプットはこの方法で作ってきた.
以下のようなアホなコード(めっちゃ計算しているようにみえるが,実は無意味なコード)も簡単に書ける.
Manipulate[Refresh[ Histogram[ {RandomVariate[NormalDistribution[0, 1], n], RandomVariate[NormalDistribution[a, 1/2], n], RandomVariate[NormalDistribution[10, 1], n], RandomVariate[LogNormalDistribution[1, 0.3], n], RandomVariate[NormalDistribution[8, 0.5], n]}, {.25}, PlotRange -> {{-3, 15}, {0, 100}}], UpdateInterval -> If[x, 0, Infinity]], {{x, False, "Run MCMC"}, {True, False}}, {{n, 300}, 1, 500, 1}, {{a, 3, "\[Mu]"}, 1, 10}]
いろいろ実験して分かったことは,ListPlotみたいな即時実行命令をRefreshするとうまくいかない,ということだ.
冗長なユーザ定義関数を割り当て(実際にはクロージャを含まないダミーでよい),遅延割り当てにすると,ちゃんとRefreshが機能する.
だからvisualizeみたいなユーザ関数を使うとうまくいくわけだ.
以上をふまえて作ったコード
(* 関数の定義 *) initialdata[n_, m1_, m2_] := {RandomVariate[NormalDistribution[m1, 5], n], RandomVariate[NormalDistribution[m2, 5], n]}; fightonce[group_] := Module[{power1, power2}, power1 = group[[1]]; power2 = group[[2]]; If[Length[power1] > 0 && Length[power2] > 0, power1 = RandomSample[power1]; power2 = RandomSample[power2]; If[(* 戦闘力を比較して勝者を残す*) RandomChoice[ {power1[[1]]/(power1[[1]] + power2[[1]]), power2[[1]]/(power1[[1]] + power2[[1]])} -> {True, False}], (* True -> 1が勝つ*) power2 = Drop[power2, 1], power1 = Drop[power1, 1]];(* If end*) ];(* If end*) {power1, power2} ]; (* update関数のほうに停止条件を書いておく. dataがなくなったらNullを返す*) visualize[data_, hight_] := Histogram[data, {1}, PlotRange -> {{0, 100}, {0, hight}}]; (* histogram を遅延評価させるために,関数化する*) (*n=50;ylim=25;sample=initialdata[n];*) Manipulate[Refresh[ If[x, sample = fightonce[sample]]; (* If文で実行する動作:UpdateInterval\[Rule]0 のときだけ,update関数を再帰的代入する*) visualize[sample, ylim], UpdateInterval -> If[x, 0, Infinity]], {{x, False}, {True, False}}, {{n, 100}, 50, 1000, 1}, {{m1, 40}, 10, 70}, {{m2, 50}, 10, 70}, Button["reset", x = False; sample = initialdata[n, m1, m2]; ylim = n/5]]
少しだけRefreshの理解が深まった(Dynamicは,まだ謎が多い).
Dynamic Models of Segregation
Dynamic Models of Segregation (Schelling 1971)をリアルタイムに表現するコードを更新したのでそのメモを残しておきます.
今回はNetLogo風に,エージェントの幸福度をリアルタイムに計算してプロットする部分を追加してみました.
Mathematica ノートブックは以下のサイト内で公開しているseg.nbというファイルをDLしてください.
使い方は,ノートブック内にも書いていますが,
- Module セルを読み込む
- 評価 [RightArrow] 動的更新の実行にチェックを入れる
- Manipulate セルを読み込む
- resetボタンを押す
- run simulationのチェックボックスをon
- 終了すると END!! が出て自動的に停止する
- 条件を変えて4.から繰り返し
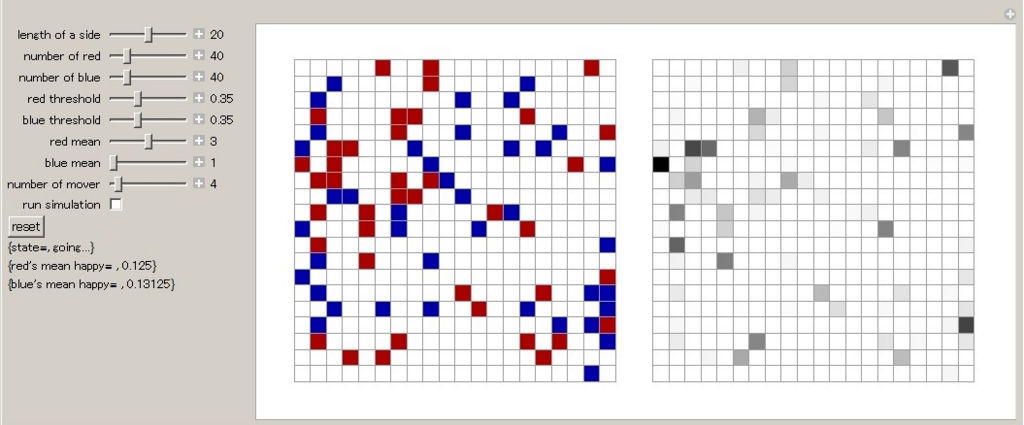
です.最終的なアウトプットはこんな感じです.
- 赤と青の個体がトーラス上をランダムに移動します
- 各個体は自分の近傍内に同色の仲間が35%以上存在すると,その位置に定着します
- 左のバーは平均的な幸福度(周りの同色エージェント割合)です
- このシミュレーションは,強い排外意識がなくても,分居が自然に生じる様子を表しています
ノートブックを読み込む段階で動的更新をonにしていると,このUIが表示されるはずですが,エラーが出る場合もあるので 最初はオフにしておき,上記の手順で動的更新を許可すれば問題ないはずです.
このnbはWolfram Demonstrations Projectで公開されているコードを参考にして作りました.
特に,GarbageCollectionByAntsというコードを参考にさせていただきました.
使用関数の定義
まずエージェントの初期配置を決める関数.size×sizeの行列上の番地でエージェントの位置を指定する. 赤エージェントの数は,rednで,赤エージェントの数は,bluenで指定する.
(*赤agent 青agentの初期配置*) initialset[size_, redn_, bluen_] := Module[{a, b, n = redn + bluen}, Developer`ToPackedArray[(* Integer型指定で高速化 *) a = RandomSample[Range[size*size], n];(* 総エージェント数だけ1次元配列から非復元抽出 *) b = Flatten[Table[{i, j}, {i, 1, size}, {j, 1, size}], 1];(* 2次元座標 *) (* 抽出した1次元配列番号を座標に変換する. 前半は赤,後半は青用 *) {Table[b[[a[[i]]]], {i, 1, redn}], Table[b[[a[[i]]]], {i, redn + 1, n}]}, Integer] ]; (* 非復元抽出で初期配置を与える. output: {{赤の位置情報},{青の位置情報}} の順で出力する initialset[size,redn,bluen][[1]] が 赤初期配置 initialset[size,redn,bluen][[2]] が 青初期配置 *)
初期グリッドに0を並べる手続きです.動的表現を使わない場合は,わざわざ定義する必要はありません.
(*初期グリッド*) zerogrid[size_] := Table[0, {size}, {size}]
エージェントの位置情報を色に変換する関数です.この関数の引数である位置情報がDynamicで更新されるのでエージェントが動いているように見える,という仕組みです.
(* agentの位置情報を検索して,可視化する関数 *) visualize[{redposi_, blueposi_}, size_] := Module[{zero1 = zerogrid[size](*Mnipulate内で指定*)}, (* Embedding agents into zero1 for visualization 引数のredposi_,blueposi_はそれぞれ「赤」と「青」の現在位置 *) Do[zero1[[ Sequence @@ redposi[[i, {1, 2}]]]] = 1, {i, Length[redposi]}]; Do[zero1[[ Sequence @@ blueposi[[i, {1, 2}]]]] = 2, {i, Length[blueposi]}]; ArrayPlot[zero1, ColorFunction -> (If[# == 0, White, If[# == 1, Darker[Red], Darker[Blue]]] &), ColorFunctionScaling -> False, ImageSize -> {300, 300}, AspectRatio -> Automatic, Frame -> False, Mesh -> All, Axes -> False] ];
全セル(トーラス空間)のムーア近傍の座標を出力する関数です.エージェントの位置毎に計算するよりも,グローバルに一回計算して,必要があるやつだけ呼び出したほうが早いんじゃないかと思って定義した関数です.計算は一回きりなので,メモリの節約にはなっていると思うのですが,実際に比較はしてません.ただ,コードの構造上はこの方法が理解しやすいと思います.
(* トーラス上に配置されたエゴのムーア近傍を出力する関数 *) moore[t_(* agent position *), size_] := Module[{m = size, p1, p2, p3, p6, p4, p7, p8, p9, network}, p6 = Table[ If[t[[i]][[2]] != m, t[[i]] + {0, 1}, t[[i]] + {0, -(m - 1)}], {i, Length[t]}]; p9 = Table[Which[(* +-している1を一般化すれば近傍の距離を自由に定義できる*) (t[[i]][[1]] != 1) && (t[[i]][[2]] != m), t[[i]] + {-1, 1}, (t[[i]][[1]] == 1) && (t[[i]][[2]] == m), t[[i]] + {m - 1, -(m - 1)}, (t[[i]][[1]] == 1) && (t[[i]][[2]] != m), t[[i]] + {m - 1, 1}, (t[[i]][[1]] != 1) && (t[[i]][[2]] == m), t[[i]] + {-1, -(m - 1)}], {i, Length[t]}]; p7 = Table[Which[ (t[[i]][[1]] != 1) && (t[[i]][[2]] != 1), t[[i]] + {-1, -1}, (t[[i]][[1]] == 1) && (t[[i]][[2]] == 1), t[[i]] + {m - 1, (m - 1)}, (t[[i]][[1]] == 1) && (t[[i]][[2]] != 1), t[[i]] + {m - 1, -1}, (t[[i]][[1]] != 1) && (t[[i]][[2]] == 1), t[[i]] + {-1, (m - 1)}], {i, Length[t]}]; p3 = Table[Which[ (t[[i]][[1]] != m) && (t[[i]][[2]] != m), t[[i]] + {1, 1}, (t[[i]][[1]] == m) && (t[[i]][[2]] == m), t[[i]] + {-(m - 1), -(m - 1)}, (t[[i]][[1]] == m) && (t[[i]][[2]] != m), t[[i]] + {-(m - 1), 1}, (t[[i]][[1]] != m) && (t[[i]][[2]] == m), t[[i]] + {1, -(m - 1)}], {i, Length[t]}]; p1 = Table[Which[ (t[[i]][[1]] != m) && (t[[i]][[2]] != 1), t[[i]] + {1, -1}, (t[[i]][[1]] == m) && (t[[i]][[2]] == 1), t[[i]] + {-(m - 1), (m - 1)}, (t[[i]][[1]] == m) && (t[[i]][[2]] != 1), t[[i]] + {-(m - 1), -1}, (t[[i]][[1]] != m) && (t[[i]][[2]] == 1), t[[i]] + {1, (m - 1)}], {i, Length[t]}]; p4 = Table[ If[t[[i]][[2]] != 1, t[[i]] + {0, -1}, t[[i]] + {0, (m - 1)}], {i, Length[t]}]; p2 = Table[ If[t[[i]][[1]] != m, t[[i]] + {1, 0}, t[[i]] + {-(m - 1), 0}], {i, Length[t]}]; p8 = Table[ If[t[[i]][[1]] != 1, t[[i]] + {-1, 0}, t[[i]] + {(m - 1), 0}], {i, Length[t]}]; network = Developer`ToPackedArray[ Table[{p6[[i]], p4[[i]], p2[[i]], p8[[i]], p9[[i]], p7[[i]], p3[[i]], p1[[i]]}, {i, Length[t]}], Integer] ];
エージェントの幸福度を計算する関数です.最小値0,最大値1です.位置情報と幸福度をセットにして出力します.
(* ムーア近傍情報に基づき幸福度(ムーア近傍内の同色エージェント割合)を計算, 位置情報に幸福度を追加 引数 agentposiは単色エージェント *) happy[agentposi_, size_] := Module[{neloca, happy3}, neloca = moore[agentposi, size]; happy3 = Table[Plus @@ Table[If[MemberQ[agentposi, neloca[[i]][[j]]], 1, 0], {j, 8}], {i, 1, Length[neloca]}]; happy3 = happy3/8;(* 同色エージェント数を *) Table[Append[agentposi[[i]], happy3[[i]]], {i, Length[agentposi]}] ]; (*入力は {{1,1},{2,1},{3,1}} のような単色エージェントの位置情報.出力は {{1,1,0.2},{2,1,0.3},{3,1,0.8}} のような 位置情報+幸福度 *)
最後にエージェントの移動を管理する関数です.設定した同色エージェント割合(閾値)に達していない場合に移動します.
(* 幸福情報に基づき,移動する visualizeの引数を生成する *) move[agents_, size_, redth_, blueth_, movern_] := Module[{preloca, zerolocate, red0, blue0, red1, blue1, k1, k2, AllocationforRed, l1, l2, AllocationforBlue}, red0 = agents[[1]]; blue0 = agents[[2]]; red1 = happy[red0, size]; blue1 = happy[blue0, size]; preloca = Flatten[{red0, blue0}, 1];(* 埋まっているセル *) zerolocate = Complement[Tuples[Range[size], 2], preloca];(*ゼロセルの番地リスト*) (*red agentからmovern人を選び動かす*非復元抽出* *) k1 = RandomSample[Range[Length[red0]], movern]; k2 = Select[k1, red1[[#, 3]] < redth &]; AllocationforRed = RandomSample[zerolocate, Length[k2]]; red[[k2]] = AllocationforRed; (*Blue agentからmovern人を選び動かす*非復元抽出* *) l1 = RandomSample[Range[Length[blue0]], movern]; l2 = Select[l1, blue1[[#, 3]] < blueth &]; AllocationforBlue = RandomSample[Complement[zerolocate, AllocationforRed], Length[l2]]; blue[[l2]] = AllocationforBlue; {red, blue} ];
さて,以上の関数をforで回すのではなく,Manipulateの中でRefreshします.
するとリアルタイムでエージェントがピコピコ動きます.このような動的表現が,MathematicaのDynamic関数によって実行できます.
以下Manipulateの中身です.
(* ver110:幸福度をlistplotでリアルタイムに更新 自動停止機能を追加,happy level モニタリングをDynamic追加 *) Manipulate[ Refresh[ If[moving, {red, blue} = move[{red, blue}, s, redth, blueth, nomove]](* 更新している部分 *); If[(Min[happy[red, s][[All, 3]]] >= redth) && (Min[happy[blue, s][[All, 3]]] >= blueth), moving = False; state = Text[Style["END !", Red, 20]], moving = moving]; state2 = Mean[happy[red, s][[All, 3]]] // N; state3 = Mean[happy[blue, s][[All, 3]]] // N; (* agentのhappy を 監視して,全員が満足したらmoving をFalseに切り替え, Dynamic[state]表示をendに変える. moving の値がFalseになると {red,blue}の更新が終わり, "run simulation"チェックボックスがoffになる*) visualize[{red, blue}, s], UpdateInterval -> If[moving, 0.01, Infinity]](* reflesh end *), {{s, 20, "length of a side"}, 10, 30, 1, ImageSize -> Tiny, Appearance -> "Labeled"}, {{redn, Floor[2*s], "number of red"}, 1, Floor[(s*s)/2], 1, ImageSize -> Tiny, Appearance -> "Labeled"}, {{bluen, Floor[2*s], "number of blue"}, 1, Floor[(s*s)/2], 1, ImageSize -> Tiny, Appearance -> "Labeled"}, {{redth, 0.35, "red threshold"}, 0, 1, ImageSize -> Tiny, Appearance -> "Labeled"}, {{blueth, 0.35, "blue threshold"}, 0, 1, ImageSize -> Tiny, Appearance -> "Labeled"}, {{nomove, Floor[(s)/5], "number of mover"}, 1, Min[{redn, bluen}], 1, ImageSize -> Tiny, Appearance -> "Labeled"}, {{moving, False, "run simulation"}, {True, False}}, Button["reset", moving = False; state = "going..."; x = initialset[s, redn, bluen]; red = x[[1]]; blue = x[[2]], ImageSize -> Medium], Dynamic[{"state=", state}], Dynamic[ListPlot[{{{1, state2}}, {{2, state3}}}, Filling -> Axis, PlotRange -> {{0, 3}, {0, 1}}, PlotMarkers -> {Red, Blue}]], SaveDefinitions -> True, TrackedSymbols :> {moving, red, blue, redn, bluen, s}, SynchronousUpdating -> True, ControlPlacement -> Left ]
なにゆえ,このManipulateでエージェントが動くのかを,ざっと解説します.
Manipulateの直接の実行対象となっている関数は Refresh[ ]です.Refresh[ ]内で,上で定義した一連の関数をループさせています.
ループさせている関数の中には,visualizeがあるので,Refreshされる度に,グラフィック出力が変化します.このRefreshするタイミングを
UpdateInterval ->で指定します.intervalが短い(上記コードでは0.01)ので,CPUさえ高性能なら,ヌルヌル動くというわけです*1.
実験としてスライダの下部にDynamic objectを2つ埋め込みました.一つはシミュレーションが停止したかどうかを示すstateです.
停止条件を満たすとここがEND!と表示されます.
もう一つが,今回修正したエージェントの幸福度(リアルタイム)です.色別の幸福度の平均値を計算してListPlotする命令をDynamicに放り込むだけでうまくいきました.
Dynamicは,誤って使用するとPCに負担がかかりすぎてカーネルが落ちるため,なかなか使いこなすのが難しい関数ですが,うまくいけば動的な表現の幅が広がるので是非
使ってみてください.
(今みなおすと,まだ無駄な計算が残っており,もっと効率化できそうです.どのあたりが修正できそうか,気づいた学生さんは授業時間内に教えてください)
*1:厳密に言えば,このオブジェクトは最速で更新されるために,インターバルの指定は無視されます.遅延評価する実行文の場合,インターバルは指定通りになります.これはRefreshの仕様です