ggplot2による事後分布の視覚化
絶対忘れるので自分用にメモしておく.
目的
Stanで推定した結果を分布のまま直接比較したい.
ggplot2用のデータフレームの作り方
流れはこんな感じ.
- Stanで推定した結果をfitに記録(CSVで記録すると結果的に遅かった.sample_file からのサンプル列の取り出しは面倒.たいした量じゃないので今回はRDataを保存してloadする).
- stanfitオブジェクトをas.data.frame()でデータフレームに変換
- パラメータの各列を1列にスタック(95年と2015年で年齢幅が違うのでindexを小細工したうえでforを回した)
- ggplot用のインデックス列を作成(年齢,性別,調査年).インデックス列は同じラベルがmcmcサンプルの数だけならぶ.今回は1000×3(chain)個.
- このときスタックの順番は男女男女とし,性別のインデックスを行方向に対応させる.
- plotしたいパラメータとインデックス列をデータフレームにまとめ,ggplotにわたす.
- ggplotのfill=で1つの枠内に男女を並べ,facet_wrap(~ age, ncol = 5)で年齢別に並べる.結果年齢別に男女比較が行列型に並ぶ
- 調査年比較は,パラメータをスタックする際に,2015,1995の順番で並べる.
コードはこんな感じ. fitに2015年度データの推定結果,fit2に1995年度データの推定結果が記録されている.
結果の一例.

暇があったら,tidyverseでもうちょっと可読性を高めたい.
Stanによる推定例:ベルヌーイ分布のパラメータ
連勝記録から勝率を推定する
ある棋士が29連勝した,というデータから,勝利確率の事後分布をMCMCで計算してみる.統計モデルの仮定は次の通りである.
毎回の勝ち負けは独立にベルヌーイ分布に従っている
ベルヌーイ分布のパラメータpの事前分布は範囲[0,1]の一様分布とする
StanとRのコードは以下の通り(コードを書くうえで松浦健太郎さんの『StanとRでベイズ統計モデリング』を参考にさせていただきました)
パラメータpの事後分布のプロット.

ベルヌーイ分布にしたがう確率変数の例を日常生活の中から見つけてみよう.
ちなみに勝率0.9で29連勝する確率は
0.929=0.04710129
である.
解析的な事後分布の導出
上述の計算機による推定と同様の結果を,手計算によって導出してみよう.
試行数1のベルヌーイ分布の確率関数は
だから,n回試行の同時確率は
である.この同時関数をパラメータθの関数として見たものが尤度関数である.
θの事前分布としてベータ分布
を仮定する.さて事後分布は
であった.ここで積の前半部分はベータ分布のカーネル
であり,後半部分はベルヌーイ分布の尤度
である.その計算結果は
ただし
となる.これはベータ分布のカーネルである.つまり事前分布としてベータ分布を指定すると,ベルヌーイ分布のパラメータの事後分布はベータ分布
となる.よって事前分布としてa=1, b=1と仮定すればθの事後分布は
である.このベータ分布をθの事後確率分布としてplotとしてみよう.まず事前分布がB(1,1)の場合.

次に事前分布がB(2, 2)の場合.

StanからWAICを計算するためのメモ
StanからWAICを計算するためのメモ
豊田本(2017)を参考に,Stanの結果からWAICを計算する方法のメモ.
テキスト198ページ記載のコードは略記のため,そのまま書き写して実行してもStanが動きません*1. 公開されたコードを参考に確率分布のパラメータを適切なブロックで定義すれば,Stanが動きます.
まずStanコード内でモデルの対数尤度を生成量(generated quantities)として定義します.
次にR上でlooパッケージを使って,Stanのサンプリング結果から対数尤度を取り出し,waic関数にわたします*2.
それぞれのコードはこんな感じです(ポイントだけ省略して書いています.実際にはデータブロックやパラメータブロックを書かなくてはいけません).
上記のGitHub Gistからの埋め込みは,Gist上で「Embed」をクリップボードにコピーしたものを
ブログのソースに張り付けるだけで完了します.
TeXstudioショートカットキーのカスタマイズ方法
オリジナルのショートカットキーを設定する方法
TeXstudio便利ですね.私は長い間 秀丸+マクロ を使っていましたが,TeX Live導入後は TeXwokrsとTeXstudioを併用しています.
さて,TeXstudioでオリジナルのショートカットキーを作成したいと思うことが時々あります.
時間がたつと,すぐにやり方を忘れてしまうので,未来の自分のためにメモを残しておきます.
例.ショートカットキーを使って,ワンストロークで
\begin{align*} & \\ & \end{align*}
といった改行込みの数式用テンプレ(環境)を入力したい,という状況を考えます.
方法の概略
「メニュー」にまず登録して,その後ショートカットキーを設定する.
手順
メニューから「オプション」→「TeXstudioの設定」を選ぶ.
「高度なオプション」にチェックを入れる(チェックしないと「メニュー項目」が出てこない)
左の列から「メニュー」を選ぶ.次に「数式」の項目から適当な一つを選び,右クリックする.
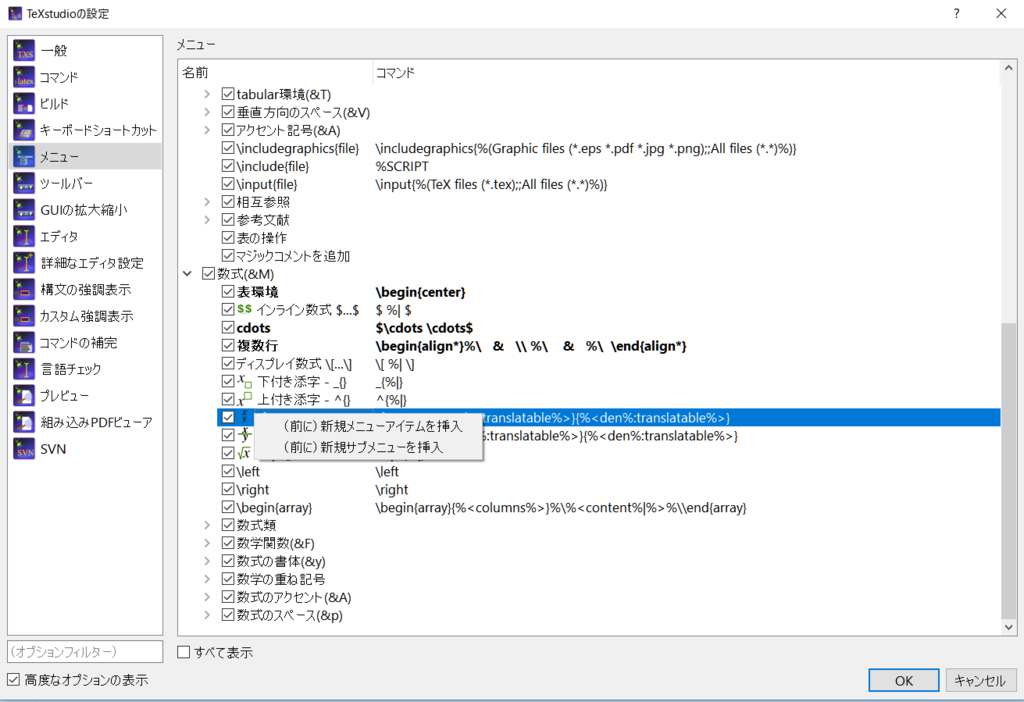
右クリックメニューから「(前に)新規メニューアイテムを挿入」を選択する.新しい項目が挿入されたら,適当な名前を入力する(今回の例では「複数行」という名前にしたと仮定します).
「コマンド」の列に,挿入したいコマンドを書く.例えば
\begin{align}%\ & \ %\ & %\ \end{align}
のように書くと,実行したときにソース上で
\begin{align*} & \\ & \end{align*}
が挿入される.メニュー設定のコマンドでは「 %\ 」が改行を意味しています. 「 %| 」で挿入後のカーソル位置を指定できます(必要がなければ指定しなくてもOKです).
- メニュー登録が完了したら,左の列で「キーボードショートカット」を選択.「数式」の項目を展開すると,今登録した「複数行」があるので「現在のショートカット」のセルをダブルクリックする.
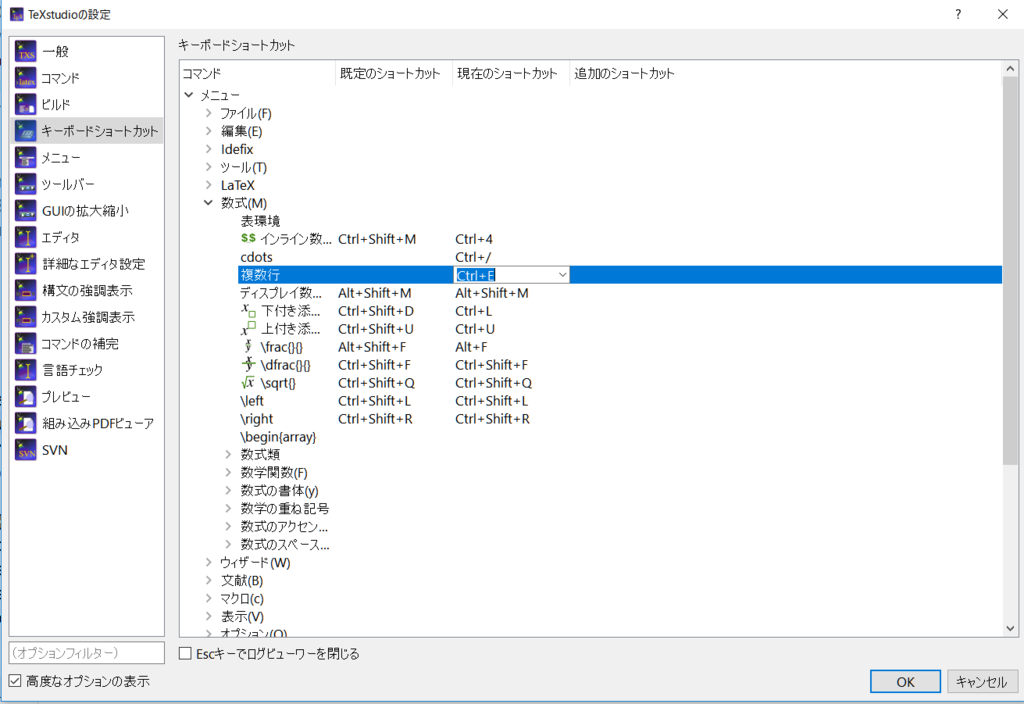
そこで自分の好きなキーを登録(例として「Ctrl + E 」を登録したと仮定します).登録後,OKボタンを押して設定を終了する.
ソース上で「Ctrl + E 」を押す.
ソースに
\begin{align*} & \\ & \end{align*}
が挿入されれば成功です.
うまくいったら,同様のやり方でよく使うコマンドを登録して,入力の手間を省きましょう(もともと登録されているものは,ショートカットキーを編集するだけでOKです.なおメニューに登録していないコマンドをショートカットキー登録する方法は知りません).
tikz-decoration
TikZのdecorationがうまくいかないので検索してみると,次のような解決策がweb上にあった.
マニュアルに記載の
\draw[decorate,decoration={coil,segment length=4pt}] (0,1) -- (3,1); \draw[decorate,decoration={coil,aspect=0}] (0,.5) -- (3,.5);
を実行するには,
\usetikzlibrary{decorations}
ではダメで,
\usetikzlibrary{decorations.pathmorphing}
まで指定しないといけないらしい.
マニュアル原典が大部すぎるため,これは確かにわかりにくい.
JAGSでWAICを計算するためのメモ
試しに計算してみたのですが,まだ細部を理解できていないので,検証用にメモを残しておきます.
豊田本2017(『実践ベイズモデリング』)にStanからWAICを計算する手順が解説されていたので,それを参考にして
JAGSから作ったサンプルでWAICを計算してみます.
例によってJAGSをRから呼び出すのにパピー4匹本のDBDA2E-utilities.Rを使います.
まずJAGS用のmodel{ }内に
# Generated quantities for (i in 1:N) { loglikelihood[i] <- log(dnorm(y[i], mu[i], 1/ (s * s))); }
などを追加して,推定したパラメータとデータを用いた対数尤度を計算します.
この場合はパラメータはmuとsです.muは説明変数に回帰しているので添え字[i]がついています.
確率密度関数は応答関数にあわせて適宜修正しましょう.
coda.samplesの結果を格納します.
mcmcCoda = coda.samples( jagsModel , variable.names=parameters , n.iter=nPerChain , thin=thinSteps )
ここから対数尤度を整形して取り出し,looパッケージのwaic関数に渡します.
こちらの記事を参考にさせていただきました.
library(loo) loglik1 <- sapply(1:N, function(i) unlist(mcmcCoda[, paste("loglikelihood[", i, "]", sep = "")])) waic(loglik1)
これでStanから計算した結果とほぼ同じWAICが出力されました.
looパッケージのextract_log_lik関数を使えばもっと簡潔になりそう.
TikZ
TikZで簡単かつ綺麗な図がかけるので,これがあれば研究の分析・報告・文章化は全てTeX+beamerだけで事足りるでしょう.
使わないとすぐに忘れそうなので,ポイントだけメモしておきます.
簡易マニュアルでも推奨しているように,最初にグリッドを書いておくと作業が大変ラクです.
これは
\draw[step=1,black!10, very thin] (0,0) grid (12, 8 );
などと入力するだけでOKです.デフォルトの座標単位が1cmなので紙の大きさに合わせて,調整すればよいでしょう.
あとはnodeで数式やプレースフォルダを配置して,drawで矢印を足していく感じ.
nodeの座標は始点位置を指定できるので,例えば
\node [right] at (0.5,7.5 )
のように書いて,調整します.基本的に[right]でいいでしょう.ただしオブジェクトを丸で囲む場合は,サークルの中心点とラベル(ノード)の中心点を合わせましょう.
矢印は
\draw[thick,-latex] (7.5 ,3 ) -- (9.5 ,2.2 ); \draw[thick,-latex] (7.5 ,1 ) -- (9.5 ,1.8 );
こんな感じで始点と終点を指定します.
狙った位置にオブジェクトをビシッと配置できるので気持ちがいいです.

まあ,パワポとどっちがラクやねんと言われれば,パワポのほうが手っ取り早い気もしますが,数式の美しさと再現可能性を考慮すればbeamer + TikZがオススメです.