自由エネルギーの計算例1
イントロ
以前,Mathlogに自由エネルギーについて書きました.
自由エネルギーは,データへのモデルのフィットを確認するために便利な指標の一つです. 特に,階層モデルでWAICの計算が煩雑な場合に,相対的に近似計算が簡単な自由エネルギーは重宝します. この指標を用いたモデル比較の意味について,単純例をつかって考えてみます.
意図
以下にいろいろと数値実験をやっていますが,知りたいことは 「データを生成する分布と一致するベイズモデルの自由エネルギー」と「データを生成する分布と一致しない最尤推定モデルの自由エネルギー」を比較するとどちらが小さいのか? です.自由エネルギーの平均値は真のモデルと周辺尤度の交差エントロピーなので,周辺尤度を真の分布と一致するように作れば,自由エネルギーの平均もその場合に最小化する,と予想します.
それではさっそく計算してみましょう
実験1
まず,パラメータリカバリ用にベルヌーイ分布$\mathrm{Bernoulli}(0.2) $にしたがうデータを生成します. つまり真のパラメータは$q=0.2$です.
100個のデータを生成します.
x <- rbinom(100,1,0.2)
中身はこんな感じです.
> x [1] 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 [43] 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0 [85] 1 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 > mean(x) [1] 0.17
このデータを次の確率モデルと事前分布で学習します. $$ X \sim \mathrm{Bernoulli}(q) $$ $$ q \sim \mathrm{Beta}(a, b) $$ つまり,ベルヌーイ分布のパラメータ$q$の事前分布がベータ分布$\mathrm{Beta}(a, b)$にしたがう統計モデルです.
この統計モデルから自由エネルギーを計算してみましょう.
サンプルの実現値が$(x_1, x_2, ... , x_n)$であるとします.
このとき周辺尤度は $$ Z_n = \frac{B(\sum x_i+a,n-\sum x_i +b)}{B(a,b)} $$ です.ここで$B(a,b)$はベータ関数 $$ B(a,b)=\int_{0}^{1} x^{a-1}(1-x)^{b-1}dx $$ です.自由エネルギーは周辺尤度の対数符号反転ですから $$ F_n=-\log Z_n=-\log \frac{B(\sum x_i+a,n-\sum x_i +b)}{B(a,b)} $$ です.
これをそのままRで定義します.
Fn <- function(x,a,b){ -1*log(beta(sum(x)+a,length(x)-sum(x)+b)/beta(a,b)) }
この自由エネルギーに,
さきほど生成したデータxを代入しつつ,事前分布のパラメータa,bを変化させて計算しましょう.
> Fn(x,a=2,b=8) [1] 46.79755 > Fn(x,a=20,b=80) [1] 46.05689 > Fn(x,a=200,b=800) [1] 45.89823
自由エネルギーFn(x,a=2,b=8)は事前分布$\mathrm{Beta}(2, 8)$
自由エネルギーFn(x,a=20,b=80)は事前分布$\mathrm{Beta}(20, 80)$
自由エネルギーFn(x,a=200,b=800)は事前分布$\mathrm{Beta}(200, 800)$
にそれぞれ対応しています(確率モデルは全て共通で$\mathrm{Bernoulli}(q)$です).ところでベータ分布の平均は$a/(a+b)$ですから $$ \frac{a}{a+b}=\frac{2}{2+8}=\frac{20}{20+80}=\frac{200}{200+800}=0.2 $$ となり,全ての事前分布の平均は,真のパラメータである$q=0.2$と一致しています.
またベータ分布の分散はパラメータの増加に対して減少するので,事前分布$\mathrm{Beta}(200, 800)$は 分散が小さいという意味で,この中では真のパラメータ$q=0.2$に,もっとも近い分布と言えるでしょう.
計算した自由エネルギーを比較すると,Fn(x,200,800)が最も小さな値を示しています.
ところで事前分布を
$$
\mathrm{Beta}(200, 800), \mathrm{Beta}(2000, 8000), \mathrm{Beta}(20000, 80000), \mathrm{Beta}(200000, 800000), ...
$$
のょうに,パラメータの比率を一定のまま大きくしていくと,どうなるでしょうか.このベータ分布は,
$q=0.2$で質点を持つようなディラックのデルタ分布に近づくことが分かります.
ここで$q=0.2$で質点を持つディラックのデルタ分布とは $$ \begin{align} d_{0.2} (q)=\begin{cases} 0 & (q\neq 0.2) \cr \infty & (q=0.2) \end{cases} \end{align} $$ と定義され $$ \int d_{0.2} ( q ) d q =1 \quad $$
$$ \int f ( q ) d_{0.2} ( q ) d q =f ( 0.2 ) $$ という性質を持つ超関数です.
では,所与のデータxのもとで,事前分布が$q=0.2$で質点を持つディラックのデルタ分布は自由エネルギーを最小化させることができるでしょうか?
そのことを確かめてみましょう.
データの平均は0.17だったので,平均位置が0.17であるようなベータ分布を事前分布として仮定します.
> Fn(x,a=1.7,b=8.3) [1] 46.83316 > Fn(x,a=17,b=83) [1] 45.93773 > Fn(x,a=170,b=830) [1] 45.63632
自由エネルギーFn(x,a=1.7,b=8.3)は事前分布$\mathrm{Beta}(1.7, 8.3)$
自由エネルギーFn(x,a=17,b=83)は事前分布$\mathrm{Beta}(17, 83)$
自由エネルギーFn(x,a=170,b=830)は事前分布$\mathrm{Beta}(170, 830)$
にそれぞれ対応しています(確率モデルは全て共通で$\mathrm{Bernoulli}(q)$です).
ここで事前分布の平均が0.2の場合の自由エネルギーFn(x,a=200,b=800)と事前分布の平均が0.17である場合の自由エネルギーFn(x,a=170,b=830)を比べてみると,
Fn(x,a=200,b=800) > Fn(x,a=170,b=830)
なので,真のパラメータに近い事前分布ではなく,データから得た平均値 に近い事前分布のほうが自由エネルギーが小さいことが分かります.なお,データの平均値はこの場合,ベルヌーイ分布からつくった尤度関数に基づく最尤推定値と一致します.
このように自由エネルギーによるモデル選択は,データを生成する真の分布を選ばないことがある,という点に注意してください.
ただしこの条件の下ではデータ数が増えれば,大数の法則によって最尤推定量が真のパラメータに確率収束するので,自由エネルギーを最小化する事前分布は真のパラメータ値を質点とするディラックのデルタ分布と一致します.
長くなったので続きます
GithubアカウントをSourcetree で認証させる方法
久しぶりにSourcetree(GitをGUI操作するためのローカルクライアント)を経由してGithub上のファイルを更新しようとしたら,「Githubの認証方式が変わったのでアクセスできません」というエラーが発生しました.
こちらを参考にトークンでの認証に切り替えたところ,うまくプッシュできるようになりました. なおトークンを発行しても,クライアントを介さずにGithubにログインする場合は,従来のパスワードでログインできています.
注意すべきは,SourcetreeのオプションでGithubアカウントを編集してパスワード部分を新たに発行したトークンに更新しても,それだけではうまくいかないところです.
上記の記事に書いてあるとおり,appdataに保存されているパスワードを削除する必要があります.なおappdataは「隠しファイルを表示」で中身を確認できます.
まだ設定してないマシンが残っているのですが,設定する頃にはやり方を忘れているはずなので,自分のためのメモでした.
ベイズ予測分布のplot
イントロ
この記事はベイズ予測分布を応答変数データのヒストグラムに重ねてplotする方法のメモです.
目的
応答変数が離散的なスケールで測定されている場合,bayesplotのppc_dens_overlay関数が使えなくて面倒くさいってことがあります.
無理矢理やると,こんな感じになり,泣けてきます.

というわけで,離散的な応答変数に連続関数の予測分布を重ねる方法を考えました.
bayesplotの設定で対応できるのかもしれませんが,どうせ後で凡例などを修正したくなるはずなので,先を見越してggplotで自作します.
準備
まずStanの出力stanfitオブジェクトからパラメータの事後分布を取り出し,
ベイズ予測分布をRで定義します.
fit <- extract(stanfit) predict<-function(x) { mean(dnorm(x,fit$mu,fit$sigma)) #確率モデルにパラメータをベクトルで代入 }
確率モデルは正規分布を仮定しています.
ここでfit$mu, fit$sigmaの長さはMCMCサンプルの個数と一致します.たとえばチェイン3で反復1500,バーンインが500と仮定すれば
MCMCサンプルの個数は$(1500-500)\times 3=3000$です.
関数predictは,確率モデルに事後分布の実現値(MCMCサンプル)を代入した値の平均なので,実質的には確率モデルの事後分布による平均(ベイズ予測モデル)の近似になっています(予測分布が解析的に出てくる場合はこの関数は必要ありません).
次に予測分布predictを使って,pdfの値を計算します.
pdf<-map_dbl(seq(0.10,0.02),predict)
seqの範囲はpdfの長さがMCMCではなくデータのサンプルサイズに一致するように適当に調整します.
なぜかといえば,ggplotで応答変数のヒストグラムとpdfの曲線を重ねたいからです.
ggplotのコ-ドは例えば次のようなものになるでしょう.
d1 <- data.frame(Level=y,yp=pdf,xaxis=seq(0,10,0.02)) ggplot(d1,aes(x=Level,y=..density..)) + geom_histogram(binwidth=1,fill="white",colour="black")+ geom_line(aes(x=xaxis,y=pdf))
結果はたとえば次のとおりです.
テスト用にサンプルサイズを小さくしたので,あまりフィットしていませんが,まあいいでしょう.
説明変数があるとき
さていろいろ試しているうちに,説明変数がある場合の予測分布の定義がよく分からないことに気づきました. パラメータが説明変数によって変化するモデル,典型的には次のような線形回帰モデルです*1.
$$ Y_i \sim N( \beta_{0} +\beta_1 X_i, s^{2}) \quad i=1,2,...,n $$
予測分布の定義を次のように書き換えます.
predict<-function(y) { dnormlist <- c() for(i in 1:n){ dnormlist <- append(dnormlist,dnorm(y,fit$b0+fit$b1*x1[i])) } mean(dnormlist) }
ここでx1が説明変数です.サンプル$i$ごとに事後分布で確率モデルを平均し,さらに最後にサンプル方向に平均します.
テスト用に応答変数が説明変数によって二峰型になるパタンを考えてみましょう
n <- 150 # sample size x1 <- c(rep(0,n/2),rep(5,n/2))#説明変数 y <-c() for(i in 1:n){ y <- append(y,rnorm(1,x1[i],1)) }
予測分布を当てはめます.
多分もっと効率のよい書き方があると思いますので気づいたら直します.
微分方程式と状態空間モデル
イントロ
微分方程式をベースにした統計モデルに関して興味深い論文を読んだので紹介します.
Naik, Prasad A., Murali K. Mantrala and Alan G. Sawyer, 1998, Planning Media Schedules in the Presence of Dynamic Advertising Quality, Marketing Science, Vol. 17, No. 3, pp. 214-235
https://www.jstor.org/stable/193228
広告のタイミングと売上の関係を時系列データで分析するという内容です. この中で特に私が注目したのは以下の部分です.
In Table 2, we briefly describe the extant models we have chosen to compare with the proposed model, namely, the models of Vidale and Wolfe [ 1957 ] , Nerlove and Arrow [1962], Brandaid [ Little 1975 ], Tracker [ Blattberg and Golanty 1978 ], and Litmus [ Blackburn and Clancy 1982 ]. It is interesting to note that these five well-known models can be cast into the same state-space form that was employed to estimate the proposed model.
筆者らは,微分方程式をベースにした理論モデルが状態空間モデルで表現できる(埋め込むことができる)と述べています.
はじめはよく分からなかったのですが,彼らのアイデアを理解するにつれ,次第に「なるほど確かにこういう方法は有用かもしれない」と思い至りました.
Naik らのアイデア
論文内で参照している five well-known models はいずれも微分方程式モデルです.Naik らのアイデアの骨子は,微分方程式を陽表的に解くのではなく,離散化した微分方程式を状態空間モデルの状態方程式として使う,というものです.
たとえばVidal-Wolfeモデルは
$$
\frac{ds}{dt}+\left( \frac{rA}{M} + \beta \right)s= rA
$$
という微分方程式なので,これを陽表的に解くと,特殊解は
$$
s=f(t)
$$
という形で表すことができます(厳密には条件分岐しますがちょっと省略して書いてます).したがってこの特殊解を決定論的パラメータとしてもつ観測誤差関数を定義すれば,カルマンフィルタでパラメータを推定したり,ベイズモデル化して予測分布を計算できます.
一方でNaikらの方法は離散化によって微分方程式を近似するため,わざわざ特殊解を特定する必要がありません.それゆえ計算がむずかしい微分方程式モデルに対して適用可能です.
integrate_ode( )を使って微分方程式をstanに計算させることも可能ですが,簡単な条件下では「微分方程式+状態空間モデル」のほうが手軽です.
*1
パラメータリカバリ
Naikらのアイデアをパラメータリカバリで確認してみましょう. まず分析用のデータは次の微分方程式 $$ \frac{dy}{dt} = r y \frac{m - y}{m}, t=0 のとき y=y_0 $$ から得た特殊解 $$ y= \frac{\exp\{ rt \}m y_0 } { m- y_0+ \exp\{ rt \} y_0} $$ に誤差を足した値であると定義します.
Rコードで書くとこんな感じです.
r <- 0.1 #増加率パラメータ 推定対象 m <- 100 # 上限 y0 <- 5 #初期値 n <- 100 #データ数. sigma <- 1 for (t in 1:n) { Y[t] <- rnorm(1, (exp(r*(t-1))*m*y0) / (m - y0 + exp(r*(t-1))*y0),sigma) }
このデータを,つぎの三つの統計モデルで予測します.
それぞれのstanコードは以下の通りです.*2
まず決定論的関数+観測誤差モデル
data { int n;//期間 real Y[n];//観測値 real y0data;//初期値 real m; } parameters { real<lower=0,upper=2> s_v; // 観測誤差の標準偏差 real<lower=0,upper=1>r;//増加パラメータ } model { target += uniform_lpdf(s_v|0,2); target += uniform_lpdf(r|0,1); target += uniform_lpdf(mu|0,100); for(i in 1:n) { target += normal_lpdf(Y[i]|(exp(r*(i-1))*m*y0data) / (m - y0data + exp(r*(i-1))*y0data), s_v); } } generated quantities{ real y_pred[n]; for(i in 1:n){ y_pred[i] = normal_rng((exp(r*(i-1))*m*y0data) / (m - y0data + exp(r*(i-1))*y0data), s_v);} }
次にローカルレベルの状態空間モデル
data { int n;//期間 real Y[n];//観測値 } parameters { real<lower=0,upper=2> s_w; // 過程誤差の標準偏差 real<lower=0,upper=2> s_v; // 観測誤差の標準偏差 real<lower=0,upper=100> mu[n];// 状態の推定値(水準成分) } model { target += uniform_lpdf(s_w|0,2); target += uniform_lpdf(s_v|0,2); for(i in 2:n) { target += normal_lpdf(mu[i]|mu[i-1], s_w);//いわゆるローカルレベルモデル } for(i in 1:n) { target += normal_lpdf(Y[i]|mu[i], s_v); } } generated quantities{ real y_pred[n]; for(i in 1:n){ y_pred[i] = normal_rng(mu[i], s_v);} }
data { int n;//期間 real Y[n];//観測値 real m;//上限 } parameters { real<lower=0,upper=2> s_w; // 過程誤差の標準偏差 real<lower=0,upper=2> s_v; // 観測誤差の標準偏差 real mu[n];// 状態の推定値(水準成分) real<lower=0,upper=1>r;//増加パラメータ } model { target += uniform_lpdf(s_w|0,2); target += uniform_lpdf(s_v|0,2); target += uniform_lpdf(r|0,1); for(i in 2:n) { target += normal_lpdf(mu[i]|mu[i-1]+r*mu[i-1]*((m-mu[i-1])/m), s_w); //状態方程式を微分方程式(ロジスティック)で代替する } for(i in 1:n) { target += normal_lpdf(Y[i]|mu[i], s_v); } } generated quantities{ real y_pred[n]; for(i in 1:n){ y_pred[i] = normal_rng(mu[i], s_v);} }
結果を比較します.
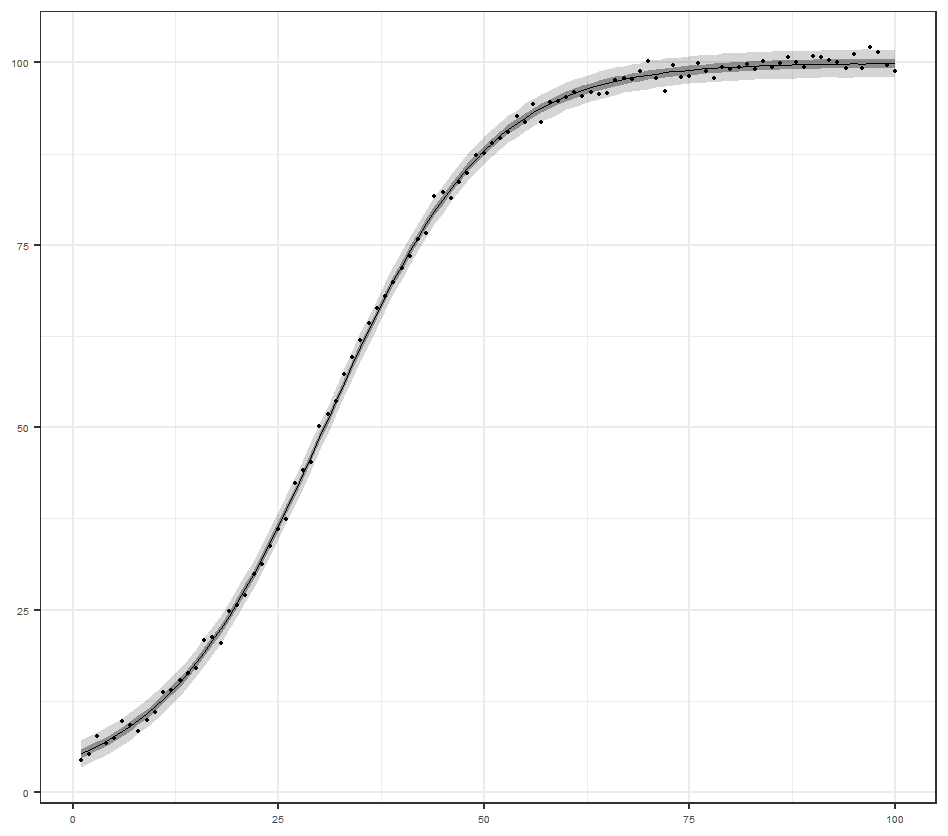
微分方程式の特殊解+誤差モデル

この統計モデルはデータを生成した真の分布と一致しているので,まあ当然の結果と言えるでしょう.
ローカルレベル状態空間モデル
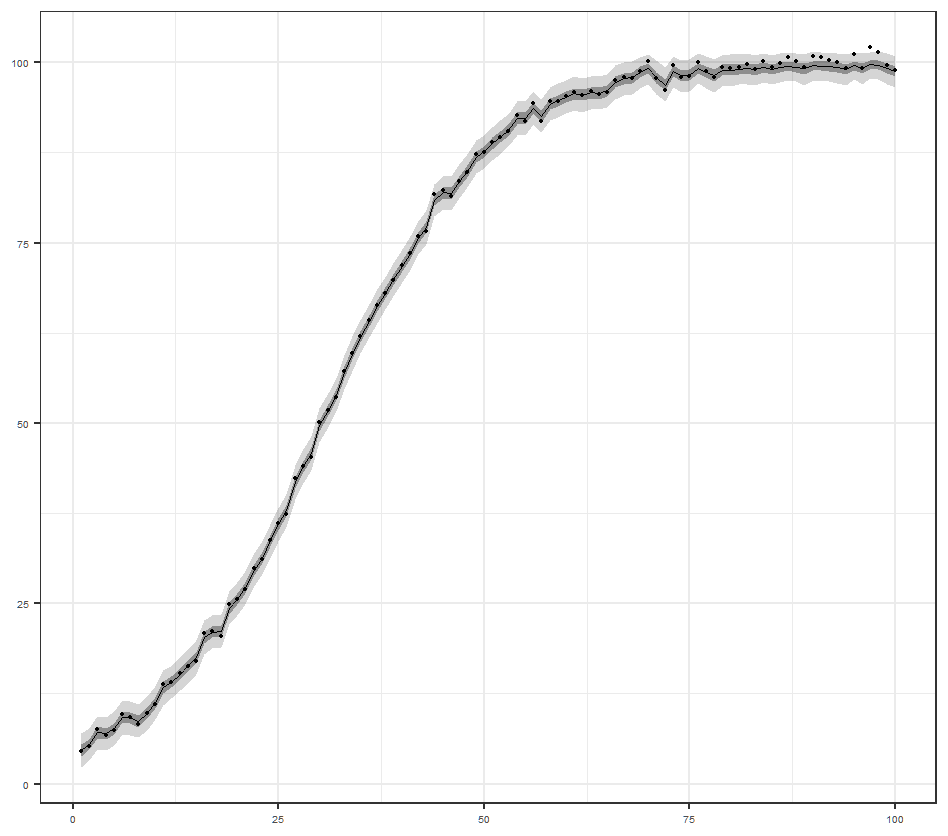
これは1期前の状態+システム誤差で現在の状態が決まるモデルです.
離散化した微分方程式を状態方程式とする状態空間モデル
今回実験してみたかったモデルです.いい感じにフィットしているようです.
各統計モデルの自由エネルギーを計算したデータへのフィットを確認します.
特殊解を使った正解のモデルと,微分方程式+状態空間モデルで近似したモデルの自由エネルギーはほぼ等しい値でした.
時間以外の説明変数があるデータのほうが,Naikらのアイデアは真価を発揮するのではないかと予想します.
ケースファンの回転数調整
PCがうるさい
なんだかPCがうるさい.HWMonitorで確認したらケースファンの回転数が常時1000RPMを超えていました.
マザーボードの設定を変えたら静かになったのですが,多分3日後にはやり方を忘れてしまうので記録を残しておきます.
4ピンではなく3ピンのコネクタだった
ケースを開けて,ケースファンのコネクタを外してみると4ピンではなく3ピンでした. 3ピンの場合は確か電圧で回転数を変更できるはずなので,BIOSもといマザボのUEFIを起動します. これはMSI社製のマザボの設定画面です.起動時にdelキーを押すとこの画面が出てきます(メーカーによってこのキーがF2だったりします).
Fan Infoから当該ケースファンに対応しているものを選択してください.
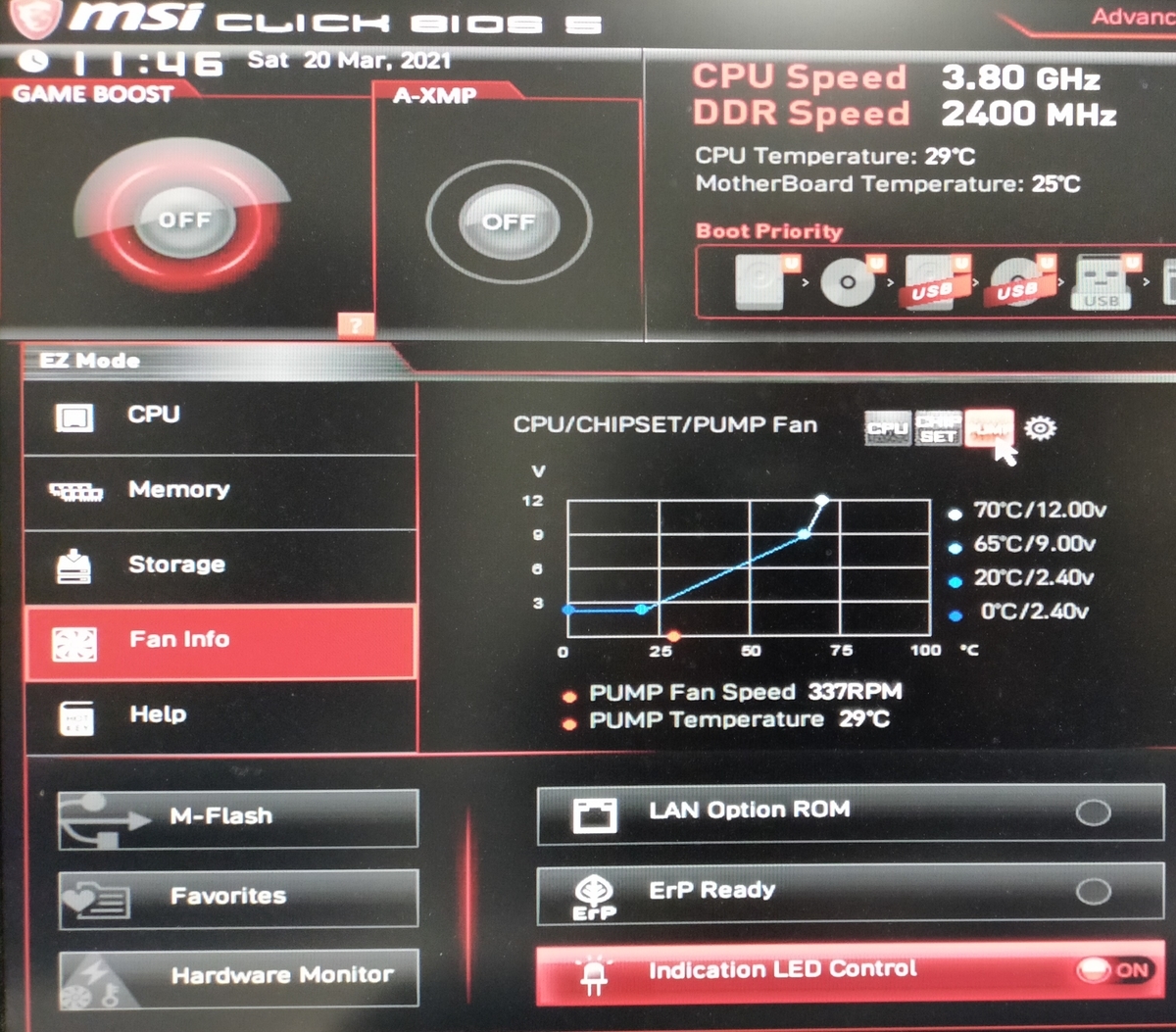
マザボの設定
ファン制御の設定を見ると,PWMになっています.PWMで制御できない3ピンコネクタを挿しているせいでしょうか,回転数が1000RPMを超えています.どうやらここが騒音の元凶のようです.
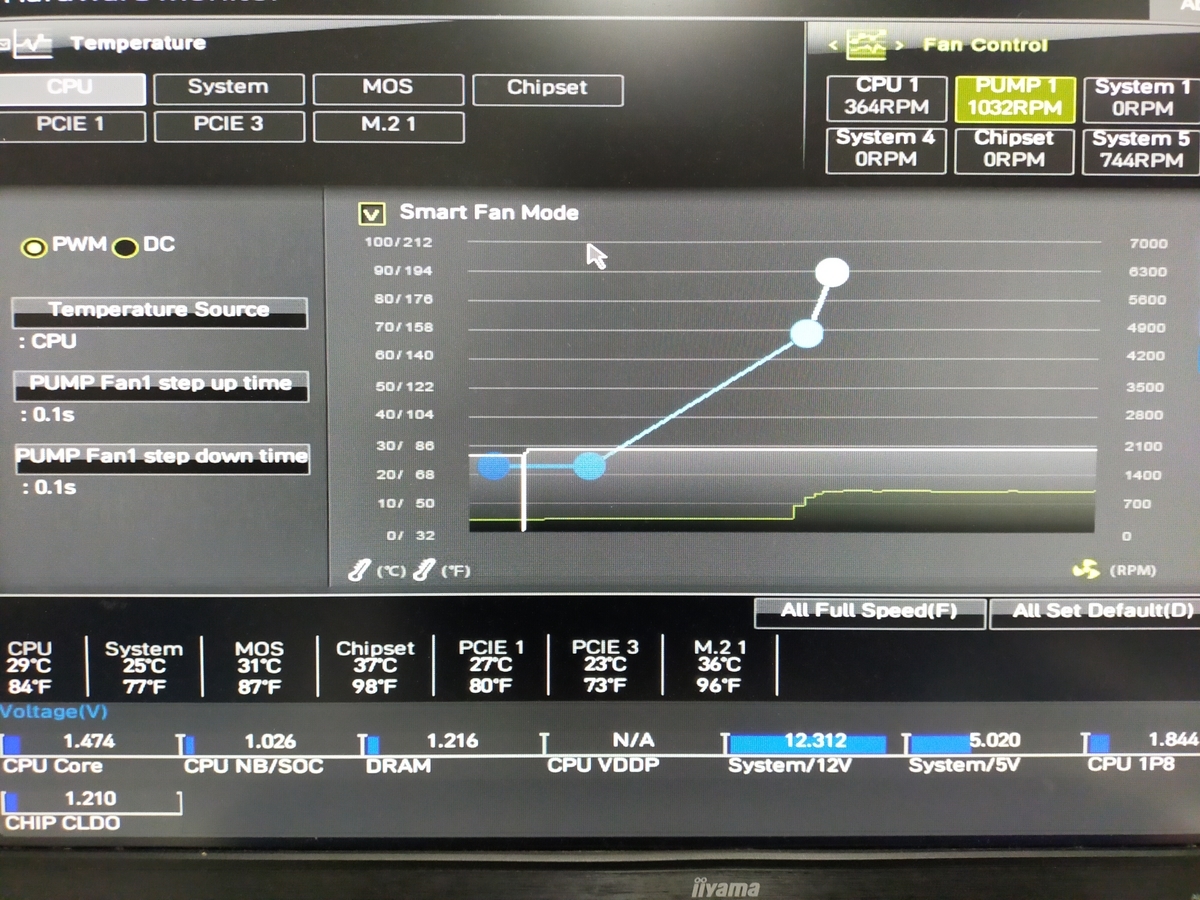
PWMからDCに変更します.340RPMに下がり,かなり静かになりました.主観的幸福感が0.5ポイントほど上昇しました.ちなみにこのマザボのUEFIは,温度別に回転数を細かく設定できます.この設定ができないマザボの場合,AutoとかSilentなどのモードを選ぶとよいでしょう.

メーカーによって多少違いはありますが,設定は似ているはずなので,ファンがうるさいなと思ったら試してみてください(ただし回転数を下げるとケース内温度は上がるので,その辺は適度に調整してください).
CPUファン
このマザボで使用しているCPUファンはサイドフロー型(横方向にファンを2個つけて風を前から後ろに流すタイプ)なのですが,ケース後方側のファンの取り付け方向が間違っていました.これをついでに直したおかげで,静かになったうえに温度も下がりました(オイ).
オブジェクトやファイル名をループ内で割り当てる(R)
ファイル名を直書きするのがめんどうくさい
50個のデータセットを使い複数のモデルで推定して自由エネルギーを計算する必要があったのでコードを書いてみました.
多分忘れるだろうから,ここに貼り付けておきます.
fevalues.m0 <- c() for (i in 1:50) { stanfit <-stan(file='model0.stan',iter=10500,warmup=500,data=f2(i),chains=4) saveRDS(stanfit,c(paste('fit/fe', i,'_0.rds', sep = ''))) fevalues.m0 <- append(fevalues.m0,-logml(bridge_sampler(stanfit,method="warp3")) ) }
ここで関数f2( )はstan用に各データセットをlist型に整形する関数です.
stan( )の引数dataに関数の出力を渡しても問題ないようです.
途中でRがコケてもstanfitが残るようにsaveRDSで逐次保存します.このときpaste( )をforループで回してデータセットに対応したファイル名を自動作成します(10個くらいなら直打ちのほうが早いでしょう.50×3個のファイル名はさすがに書く気がしない).
saveRDS内でpaste( )を使っても問題ないようです.
stanfitは上書きされて1つしか残らないため,メモリ不足でRがクラッシュすることを防ぎます(多分)
計算した統計量(ここではブリッジサンプリングから計算した自由エネルギー)は空のベクトルfevalues.m0にappendしていきます.
モデルを変える場合は,stan( )のモデル部分だけ変え,上記のfor文をコピペして使い回します.
1回のループにまとめることもできますが,かえって可読性が悪くなると判断しました.
このくらいで分割した方が,数ヶ月後の自分には理解しやすいでしょう.
呼び出したstanfitからの計算
readRDSで保存したstanfitを使ってbridge_sampler( )を適用すると,「modelがないぞ」とrstanに怒られます.
「コンパイルしたモデルは保存する設定にしとるやろがい!」と悪態をつきたくなる気持ちをぐっとこらえ,stanfitに対応したモデルをchains=0で再コンパイルします(これは時間はかかりません).
mod<-stan(file='model0.stan',iter=10500,warmup=500,data=f2(i),chains=0) -logml(bridge_sampler(stanfit,mod,method="warp3"))
これなら計算してくれます.
他に解決策があるのかもしれませんが,今回はこれでOKとします.
数理モデル本の続編を書きました
はじめに
『その問題,やっぱり数理モデルが解決します』をベレ出版さんから刊行しました.以下,その内容をざっと紹介します.


その問題、やっぱり数理モデルが解決します: データ時代を生き抜くための数理モデル入門
- 作者:宏, 浜田
- 発売日: 2020/09/14
- メディア: 単行本
本書は次の4つのパートから構成されます.
はじめから順番通りに読んでもいいし,興味のあるパートから読んでも構いません.
前作『その問題,数理モデルが解決します』と同様に,登場人物達の対話を通して数理モデルを紹介します.世界観は共通ですが,内容は独立しているので,今作から読み始めていただいても問題ありません.数学の難易度は前作よりも少し易しくなるよう心がけました.
対象読者
本書の読者として以下のような方を想定しています.
特徴
「数理」モデルの理解はなかなか困難です.そこでなるべく分かりやすく,かつ,数式はちゃんと使いつつ数理モデルの使い方や作り方を紹介するために,この本を書きました.おそらく,キャッチーな表紙からは想像できないほど本書にはたくさんの数式が登場します.しかしこれにはちゃんとした理由があります. 1つの計算過程を省略せずに書くためには,必然的にたくさんの式が必要です.逆に言うと,途中の変形ステップを省略せずに式がたくさん書いてある本ほど,実は簡単に読めるのです.
多くの初学者は,数式間で省略されたステップが理解できずに挫折します.ですので本書は,(前作同様に)可能な限り式変形を丁寧に書くよう心がけました*2.
各章のタイトル・難易度・トピック
| タイトル | 難易度 | トピック |
|---|---|---|
| 第1 章 しっくりこない数式の読み方とは? | ☆ | 総和記号、添え字の読み方、平均値 |
| 第2 章 確率密度関数ってなに? | ☆ | 定義の読み方、グラフの描き方、パラメータの役割 |
| 第3 章 確率と積分の関係とは? | ☆ | 正規分布、測定誤差、確率密度関数のつくり方 |
| 第4 章 モデルってなに? | ☆☆ | 競争市場、需要量、代替財、均衡価格、独占モデル |
| 第5 章 競争で損をしない戦略とは? | ☆☆ | 複占モデル、ゲーム理論、ナッシュ均衡 |
| 第6 章 自分でモデルをつくる方法 | ☆ | モデルのつくり方、モデルの一般化、モデルで自由に遊ぶ |
| 第7 章 先手が有利な条件とは? | ☆☆ | 後ろ向き帰納法、展開形ゲーム、情報集合 |
| 第8 章 競争に負けない価格設定とは? | ☆☆ | 代替性、モデルのバリエーション、検証 |
| 第9 章 売り上げを予測するには? | ☆☆ | 回帰分析、最小2乗法、微分、偏微分 |
| 第10 章 確率モデルでデータを分析するには? | ☆☆☆ | 確率変数、OLS推定量、正規分布の再生性 |
| 第11 章 仮説検定ってどうやるの? | ☆☆☆ | 推定量の確率分布、t分布、解釈の注意点 |
| 第12 章 観測できない要因の影響を予想するには? | ☆☆ | 欠落変数バイアス、期待値、不偏推定量、固定効果 |
| 第13 章 アプリの利用者数を予測するには? | ☆☆ | 微分方程式、置換積分法、変数分離形 |
| 第14 章 広告で販売数を増やすには? | ☆☆☆ | 1階線形微分方程式、積分因子 |
メッセージ
私は大学院に入るまでは,「数学は自分の人生に無用だ」と考えていました. しかし今では数理モデルを勉強したり数理モデルを使うことは,人生に欠かせない楽しみの一つです. 本書をきっかけに,数理モデル(数学)っておもしろいかも,と思っていただけたら望外の喜びです.
以下,各章の概要です.ちょっと長いので気になる人だけどうぞ.
各章の内容
第1 章 しっくりこない数式の読み方とは?
難易度☆ 総和記号、添え字の読み方、平均値
ときどき,$\sum$が苦手だ,という学生さんの声をよく聞きます. $$ \sum_{i=1}^{n}x_i=x_1+x_2 + \cdots +x_n $$ は分かるんだけど, $$ \sum_{i=1}^{n}a=an $$ は,なんかしっくりこない,と.
第1章ではこのような総和記号の意味からはじめて,《分かったような分からないようなしっくりこない数式》に出会ったときに,どうやってその式を理解するのか,その一般的な方法を解説します.
第2 章 確率密度関数ってなに?
難易度☆ 定義の読み方、グラフの描き方、パラメータの役割
統計学や確率論のテキストを開いたところ,
次の2つの条件を満たす関数$f: R \to R$を確率密度関数という.
- 任意の$x \in R$について$f(x)\ge 0$
- $\int_{-\infty}^{\infty} f(x)dx=1$
といった定義がいきなり出てきて,「ちょっとなに言ってるかわからない」と思ったことはありませんか?
2章では確率密度関数を例に,抽象的な定義を理解する方法を解説します.
統計や数学を学ぶ上で《自分で具体例をつくる》ことはとても大切です. ここでは式を単純化したり,コンピュータを使ってグラフを描いたり,条件を変えて比較したりさまざまな試行錯誤 を通して抽象的概念を理解する方法を学びます.
第3 章 確率と積分の関係とは?
学生の頃,確率密度関数を計算してたら「4.023」や「5.251」のように1よりも大きな値が出てくるので,「積分したら1になる関数なのに,なんでこんな値が出てくんねん」と頭をひねったことがありました.よく考えれば別に不思議なことではないのですが,一見奇妙に思える理由を説明しつつ,積分の直感的な意味や確率密度関数を解説します.
積分と確率の一致が納得できると,確率論の世界が目の前にぱっと広がります.
第4 章 モデルってなに?
難易度☆☆ 競争市場、需要量、代替財、均衡価格、独占モデル
モデルとはなにか,という基本的な話を競争市場を例に説明しました.途中までは数式なしで,最後にほんの少し数式(独占モデル)が出てきます.数式は現実的な『意味』が与えられると,世界を表現する豊かな言葉に変化します.昔,師匠から「数理モデルの勉強を始めてから,無機質な数式が急に色めきたって見えた.まるで白黒の世界からカラーの世界に変わったような気がした」という話を聞かせてもらったことがあります*3.そんな瞬間を読者にも感じてほしいなと思ってこの章を書きました.
第5 章 競争で損をしない戦略とは?
『経済学のためのゲーム理論入門』(ギボンズ)でクールノーの複占モデルを初めて知ったとき,「このモデル,すごい!完璧や!」と感動しました.一般に,モデルのよさは $$ モデルのよさ=\frac{インプリケーションの豊かさ}{モデルの複雑さ} $$ で評価できます.複雑すぎるのもよくないし,かといって単純すぎてインプリケーションが自明なモデルもよくありません.単純さとインプリケーションの豊かさを両立させることは困難ですが,クールノー複占モデルは見事なバランスで,両者を実現しています*4.ここではそんなゲーム理論の名作,クールノー複占を例にシンプルなモデルの作りかたを解説します.
第6 章 自分でモデルをつくる方法
難易度☆ モデルのつくり方、モデルの一般化、モデルで自由に遊ぶ
モデルを拡張したり一般化する方法を実例をもとに解説しています.このあたりの話は既存のテキストだと「できて当たり前」の操作として扱われることが多いのですが,自分でモデルをつくるときには,この計算のプロセスを詳しく示す必要があるなと思ってこの章を書きました. 花京院くん曰く,モデルをつくることは「カツカレー」を作ることに似ているそうです.はたしてその意味は?
第7 章 先手が有利な条件とは?
難易度☆☆ 後ろ向き帰納法、展開形ゲーム、情報集合
モデルの拡張やヴァリエーションを複占モデルの展開形で説明します. 4章からスタートして,5,6,7,8章と独占・複占モデルを主題とする変奏曲が続きます. 新しいキャラクターも登場します.
第8 章 競争に負けない価格設定とは?
難易度☆☆ 代替性、モデルのバリエーション、検証
ひきつづきモデルの拡張やヴァリエーションを複占モデルで説明します. ここでは戦略集合が『生産量』から『価格』に変わります.やはりコアになっているのは独占モデルで,ここが最後のバリエーションです. データによるモデルの検証についても少し考えながら,次章の統計学の導入へと続きます.
第9 章 売り上げを予測するには?
もっとも基本的なデータ分析法のひとつである回帰分析とその原理にあたるOLSを解説します. 微分がよく分からない,忘れてしまったという人はこの章で確認してください.
第10 章 確率モデルでデータを分析するには?
ここでは確率変数を明示的に導入して,誤差項の分布から推定量の分布を導出します. 回帰分析を確率モデルとして構成することで,係数の検定(次章)が可能となります
第11 章 仮説検定ってどうやるの?
難易度☆☆☆ 推定量の確率分布、t分布、解釈の注意点
回帰係数の検定を解説します. OLSは分かるけれど,係数の検定はよくわからない,という読者に向けて書きました. 確率変数同士を合成して新たに確率変数をつくる,という流れがイメージできると推定量の分布がなぜ正規分布やt分布にしたがうのか分かります.
第12 章 観測できない要因の影響を予想するには?
難易度☆☆ 欠落変数バイアス、期待値、不偏推定量、固定効果
欠落変数バイアスについて解説します.単にそういうバイアスがあるんだよって話ではなく,陽表的な関数として導出する過程を示しています. 本書では触れませんでしたが因果推論や条件付き期待値回帰を勉強する場合にバイアスの理解が役に立ちます.
第13 章 アプリの利用者数を予測するには?
微分方程式モデルの基礎を説明します.積分の計算方法を知らない,あるいは習ったけど忘れてしまった,という方はこの章で復習してください. 置換積分の計算は,確率変数の計算にも役立つので,ぜひ紙に式を書いて納得してください. 積分の計算は面倒ですが,この計算によって確率論の理解がぐっと深まります.
第14 章 広告で販売数を増やすには?
最後は広告の効果を分析する微分方程式モデルの紹介です.Vidal & Wolfe(1957)の古典的な論文をベースに,新キャラクターのヒスイが発展的なモデルを提案します. 異なる広告タイプを比較するために積分を利用するあたりが面白いモデルだと思います.13、14章では積分が大活躍します.
最後まで読んでいただき,どうもありがとうございました.
*1:数理モデルは,数学を使って現象を表現・説明・予測する方法の総称であり,観察した現象から本質を見抜く洞察やデータを分析するための指針(理論)を与えてくれます.現象が成立するメカニズムを数理モデルで特定できれば,不確実な未来を予測できます.コロナウィルスの感染症対策でSIRモデルおよびその拡張的数理モデルは,しかじかの仮定の下で感染者数はこうなると明確な予想を導きました.
*2:逆にいえば,既に数学を使った議論に慣れている中級者以上の読者には,少しもの足りないかも知れません.もう少し難易度が高くてもOKかつ,ベイズ統計モデルに関心のある方は,『社会科学者のためのベイズ統計モデリング』をご覧ください.共著者の清水さんによる紹介記事はこちらです
*3:私は師匠のつくった数理モデルの論文を読んだとき,最初は意味が分からなかったのですが,計算を繰り返すうちに小さな世界で人が動いている様子を想像できました.いえ,酔っ払ってヘンなモノを見たわけではありません
*4:ゲーム論のモデルにはたくさんの名作がありますが,クールノー複占は個人的にはベスト3に入るくらい好きなモデルです.ちなみに,この章を書くためにクールノー複占をゲーム理論で最初に表現した人が誰かを調べてみました(クールノーはゲーム論が生まれるずっと前に複占モデルを定式化していました).どうやらギボンズよりもフリードマンの方が早かったようです