Income Segregation

www.jstor.org

この論文を読んでいて，Income Segregation と Race Segregation　を組み合わせて表現するコードを思いついたので，メモを残しておきます．

以前から，シェリングのsegregation modelにエージェントの所得情報を別のレイヤーで表示させる，というアイデアを思いついていました． ただ，面倒な割にインプリケーションも少ないかなと思って，今日まで実装するに至りませんでした．

しかし，Reardonのような実証論文があるということは，理論的な挙動を把握するためのプロトタイプを作ってみるのも悪くないかと思い，今回試しにやってみた次第です．

例によってコードはMathematicaでちゃちゃっと書きます*1.

所得情報のArrayPlot

まずエージェントの所得情報をArrayPlotするModuleを考えます．最初にエージェント毎に所得ベクトルを生成します．

(* income　の初期情報を与える *)
income[redn_, bluen_, mred_, mblue_] := Module[{sigma = 1},
   {RandomVariate[LogNormalDistribution[mred, sigma], redn],
    RandomVariate[LogNormalDistribution[mblue, sigma], bluen]}
   ];

次に位置情報の初期配置を与えます．

(*赤agent 青agentの初期配置*)
initialset[size_, redn_, bluen_] :=
  Module[{a, b, n = redn + bluen},
   Developer`ToPackedArray[(* Integer型指定で高速化 *)
    a = RandomSample[Range[size*size], n];(* 総エージェント数だけ1次元配列から非復元抽出 *)
    b = Flatten[Table[{i, j}, {i, 1, size}, {j, 1, size}], 1];(* 2次元座標 *)
    (* 抽出した1次元配列番号を座標に変換する．　前半は赤，後半は青用 *)
    {Table[b[[a[[i]]]], {i, 1, redn}], 
     Table[b[[a[[i]]]], {i, redn + 1, n}]}, Integer]
   ];
(* 非復元抽出で初期配置を与える． output: {{赤の位置情報}，{青の位置情報}} の順で出力する*)

これは以前に解説した関数と同じです．

次に所得情報を位置情報に対応させてArrayPlotするための関数を定義します．

(* 所得情報をplotする関数 *)
visualize2[{redposi_, blueposi_}, incomelist_, size_] :=
  Module[{zero1 = zerogrid[size], redincome, blueincome(* 
    sizeは　Manipulate内で指定*)},
   (* Embedding agents into zero1 for visualization 
   引数のredposi_,blueposi_はそれぞれ「赤」と「青」の現在位置　*)
   redincome = incomelist[[1]];
   blueincome = incomelist[[2]];
   Do[zero1[[ Sequence @@ redposi[[i, {1, 2}]]]] = redincome[[i]], {i,
      Length[redposi]}];
   Do[zero1[[ Sequence @@ blueposi[[i, {1, 2}]]]] = 
     blueincome[[i]], {i, Length[blueposi]}];
   ArrayPlot[zero1, ImageSize -> {300, 300}, AspectRatio -> Automatic,
     Frame -> False, Mesh -> All, Axes -> False]
   ];

ここではゼロのならんだグリッドに，エージェントの位置に応じて所得値を割り当てます．例えばもとの3次正方行列のゼログリッドが

0,0,0,

0,0,0,

0,0,0

だった場合に，3人分の所得{5,3,2}を位置情報{{1,3},{2,1},{3,3}}に割り当てると

0,0,5,

3,0,0,

0,0,2

という出力を得ます．後は所得の大小に応じてグレーに色分けしてプロットする必要があるのですが，ArrayPlotのデフォルト設定をそのまま利用します． 実はデフォルトで数字の大小に応じたグレースケールに変換して，Plotしてくれるのです（便利やー）．

この部分，おもしろくない割に最初から作ると面倒なので，助かります *2

さて，ここで注意すべきは，次の点です．

• 位置情報の動的更新をせずに，所得値の情報だけ正しい位置に表示できるかを確認する．
• これができたら，動的更新のModuleに組み込む*3

次にパネルを二つ並べるために， GraphicsRowをManipulateのオブジェクトとして指定します．

GraphicsRow[{
  ArrayPlot[{Table[Random[], {5}]}],
  ArrayPlot[{Table[Random[], {5}]}]
  }]

括弧の数に注意しましょう．できあがりはこんな感じです．

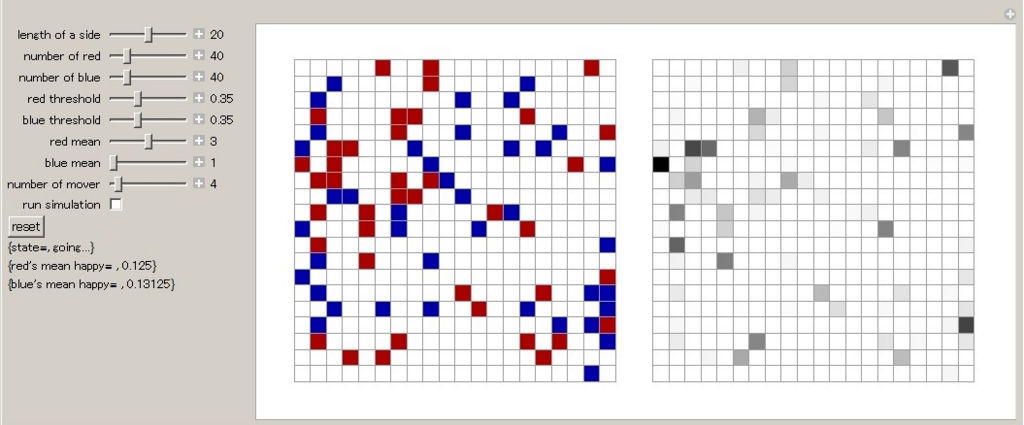
右のパネルが所得値を表しています．黒いほど高額所得です．

実行すると二つのパネルが同期して動きます．

人種に関する選好だけを持っていたとしても，人種間の所得分布に差があるとき，結果としてincome segregation(金持ちが金持ち同士で固まって住む)が生じる様子が分かります．これは統計的差別がもたらす意図せざる結果の一種と解釈することも可能です．

ただし，ここまでの結論は計算しなくてもほぼ自明なので，今後は

1. 片方の人種だけに同人種への選好があっても，income segregationが生じるのか？
2. 人種選好がincome segregationに及ぼす影響の推定
3. 逆に人種選好はないが，incomeへの選好だけあるとき，人種間segregationはどの程度生じるのか
4. 地価上昇ダイナミクスを取り入れると，人種間不平等がどのくらい高まるのか

などを考えてみようと思います．

*1:なお，自分で試してみたい学生は，授業で配布したサンプルコードをいきなり修正せず，追加すべきModuleだけプロトタイプを作り，実験してから組み込むようにしてください

*2:こういう内蔵関数が豊富なところが，Mathematicaのいいところだなあ

*3:はじめてシミュレーションに取り組む学生は，1ステップずつ作業を進めてください．複数のクロージャをまとめて更新すると，どこでエラーが出たか分かりません．慣れるまでは，1つずつエラーを直しながら進めてください．面倒なようですが，このほうが結果的に早いのです．さもなければバグがどこにあるか一日中探さなくてはなりません．はじめのうちはバグを直すより，バグを見つける方が難しいのです