自由エネルギーの計算例2

実験2

前回の続きです．

データを生成する分布として次のような複合分布を考えます．

$$ X \sim \mathrm{Bernoulli}(q) $$ $$ q \sim \mathrm{Beta}(a, b) $$ これはベルヌーイ分布のパラメータ$q$の事前分布がベータ分布$\mathrm{Beta}(a, b)$にしたがう複合分布です．

パラメータ$q$を消去すればこの複合分布は ベータ2項分布 $$ X \sim \mathrm{Betabinomial}(1,a,b) $$ と一致します．

このベータ2項分布からデータを生成し，「正しい」統計モデルで分析します．

つまり $$ X \sim \mathrm{Bernoulli}(q) $$

$$ q \sim \mathrm{Beta}(a, b) $$ というベイズ統計モデルを仮定して自由エネルギーを計算したらどうなるかを実験して確かめます．　

まずデータを生成するためにRのextraDistrパッケージを使い，ベータ2項分布にしたがう確率変数の実現値を100個つくります．

> library(extraDistr)
> rbbinom(100, 1, alpha = 2, beta = 8)
  [1] 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0
 [43] 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0
 [85] 1 0 0 0 1 1 0 0 0 0 0 0 0 0 1 0

このデータを使って自由エネルギーを計算します．

> Fn(x,a=2,b=8)
[1] 49.84582
> Fn(x,a=20,b=80)
[1] 48.97739
> Fn(x,a=200,b=800)
[1] 48.69709

念のため，Mathematicaでも同種のデータを生成します．

In[1]:= (* ベータ2項分布からの実現値生成 *)
x = RandomVariate[ BetaBinomialDistribution[2, 8, 1], 100]

Out[1]= {1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, \
1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, \
0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, \
0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1}

In[2]:= Mean[x]

Out[2]= 9/50

自由エネルギーを定義して計算してみましょう．

In[4]:= FEnergy[x_, a_, b_] :=
  N[-1*Log[Beta[Total[x] + a, Length[x] - Total[x] + b]/Beta[a, b]]];

In[5]:= 
FEnergy[x, 2, 8]
FEnergy[x, 20, 80]
FEnergy[x, 200, 800]
FEnergy[x, 2000, 8000]
FEnergy[x, 20000, 80000]

Out[5]= 48.3529
Out[6]= 47.5336
Out[7]= 47.3005
Out[8]= 47.271
Out[9]= 47.268

さすがはMathematica．パラメータが20000，80000でも余裕で計算してくれます（Rだと200，800が限界でそれ以上は計算してくれない．そういうとこやぞ）．

どちらも同じような結果になりました． さてデータを生成する分布として$\mathrm{BetaBinomial}(n=1,a=2,b=8)$を仮定していますが， データから計算した平均の最尤推定値は9/50です．

次に事前分布の平均値が9/50になるようなモデルの自由エネルギーを計算してみます．

N[FEnergy[x, 180000, 820000], 10 ]
N[FEnergy[x, 1800000, 8200000], 10 ]
N[FEnergy[x, 18000000, 82000000], 10 ]

47.13939868
47.13935368
47.13934918

真のモデルよりも小さい？　 自由エネルギーは確率変数なので，データの出方によってばらつきがあります．以上の計算をふまえ，データを複数回生成することで自由エネルギーの平均を比較します．

out <- c()#真の事前分布beta(2,8)の自由エネルギー
for(i in 1:3000){
  x <- rbbinom(1000, 1, alpha = 2, beta = 8)
  out <- append(out,Fn(x,a=2,b=8))
}

out2 <- c()# 事前分布beta(20,80)の自由エネルギー
for(i in 1:3000){
  x <- rbbinom(1000, 1, alpha = 2, beta = 8)
  out2 <- append(out2,Fn(x,a=20,b=80))
}

out3 <- c()# MLの自由エネルギー
for(i in 1:3000){
  x <- rbbinom(1000, 1, alpha = 2, beta = 8)
  out3 <- append(out3,-1*log(mean(x)^(sum(x))*(1-mean(x))^(length(x)-sum(x))))
}

結果を比較すると......

最尤法モデル＜ベイズモデル beta(20,80) ＜ベイズモデル beta(2,8)　

となりました． 真の分布と同じ統計モデル（確率モデル＋事前分布）の平均自由エネルギーより，最尤推定モデルに近いベイズモデルや最尤推定モデルの平均自由エネルギーのほうが小さいことが分かりました*1．

統計モデルが真の分布に一致している場合よりも，事前分布が最尤推定値に質点を持つディラックデルタ分布に近い方が，この条件下では自由エネルギーの平均値が小さくなっています．このことから自由エネルギーによるモデル選択は，データを生成した分布よりも，観察したデータそのものに尤度の意味で近い統計モデルを選んでいるらしいと考えられます．なぜこうなってしまうのでしょうか？引き続き考えてみます．

実験3

さきほどの実験では，$\mathrm{BetaBinomial}(n=1,a=2,b=8)$からデータを生成しましたが，そもそもこのデータでは複合分布を周辺化した結果がベルヌーイ分布と一致するので例としては特殊すぎた可能性があります．

違う条件で計算してみるとどうなるのでしょうか？ 自由エネルギーによるモデル選択は最大対数尤度による選択と一致するのでしょうか？

実験3の設定は次の通りです．はじめにデータを $$ X \sim \mathrm{Poisson}(\lambda) $$

$$ \lambda \sim \mathrm{Gamma}(a, b) $$ という結合分布から生成します．よく知られているように，この仮定の下で$\lambda$を周辺化すると，$X$は負の2項分布に従うことが知られています． したがってデータを $$ X \sim \mathrm{NegativeBinomial}(a, 1/(b+1)) $$ から生成したと考えても同じことです． 以下では$a=1, b=3$を仮定してデータを生成します（$n=100$のデータを作りました）．

In[3]:= x = RandomVariate[NegativeBinomialDistribution[1, 0.25], 100]
Out[3]= {5, 0, 2, 1, 3, 5, 2, 9, 2, 0, 8, 2, 13, 2, 2, 0, 6, 0, 3, 6, \
4, 0, 1, 4, 1, 19, 2, 8, 0, 1, 0, 1, 5, 4, 3, 0, 5, 0, 9, 0, 3, 0, \
17, 1, 10, 5, 2, 8, 1, 0, 2, 2, 4, 0, 0, 9, 2, 0, 0, 3, 3, 2, 5, 0, \
0, 2, 0, 2, 1, 1, 4, 0, 7, 0, 1, 21, 5, 6, 0, 0, 0, 7, 4, 0, 0, 0, 0, \
0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0}

このデータをベイズモデル $$ X \sim \mathrm{Poisson}(\lambda) $$

$$ \lambda \sim \mathrm{Gamma}(a, b) $$ で学習して自由エネルギーを計算します． するとこのベイズモデルの自由エネルギーは $$ F_n=-\log\Gamma\left(\sum x_i+a\right) +\log \Gamma(a)+\sum \log x_i ! -a\log b +\left(\sum x_i +a\right)\log (n+b) $$ です（浜田・石田・清水2019: 111）．

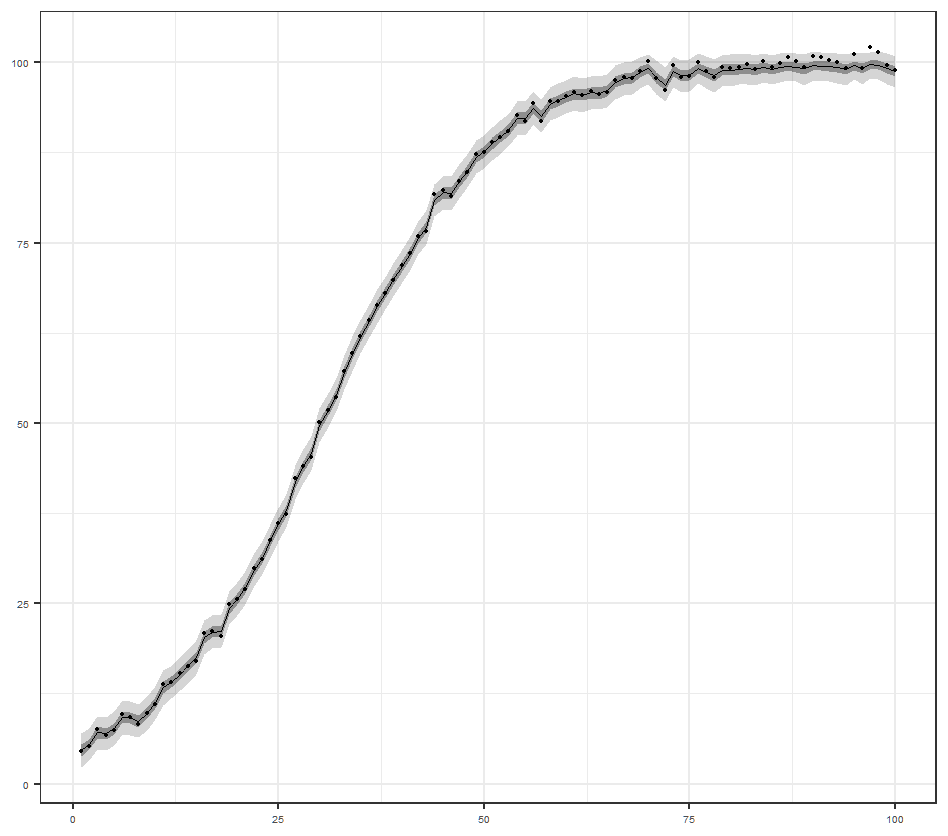
自由エネルギーの引数はデータ$x_1, x_2, ... x_n$とパラメータ$a, b$です．このうちデータと片方のパラメータの真値$a=1$が与えられたとして，$b$の変化による自由エネルギーの変化を確認してみましょう．

自由エネルギーの変化

データを生成したパラメータは$a=1, b=3$ですから，$b=3$のとき最も小さくなることを予想していましたが，全く違う箇所で最小化しているようです．

次にデータを生成した負の2項分布ではなく，ポアソン分布を確率モデルとして使った場合の自由エネルギーを計算します．事前分布としてデータの平均の最尤推定値に質点をもつようなディラックデルタ分布を仮定します．つまりポアソン分布で最尤推定した場合の対数尤度の符号反転を自由エネルギーとして定義します．

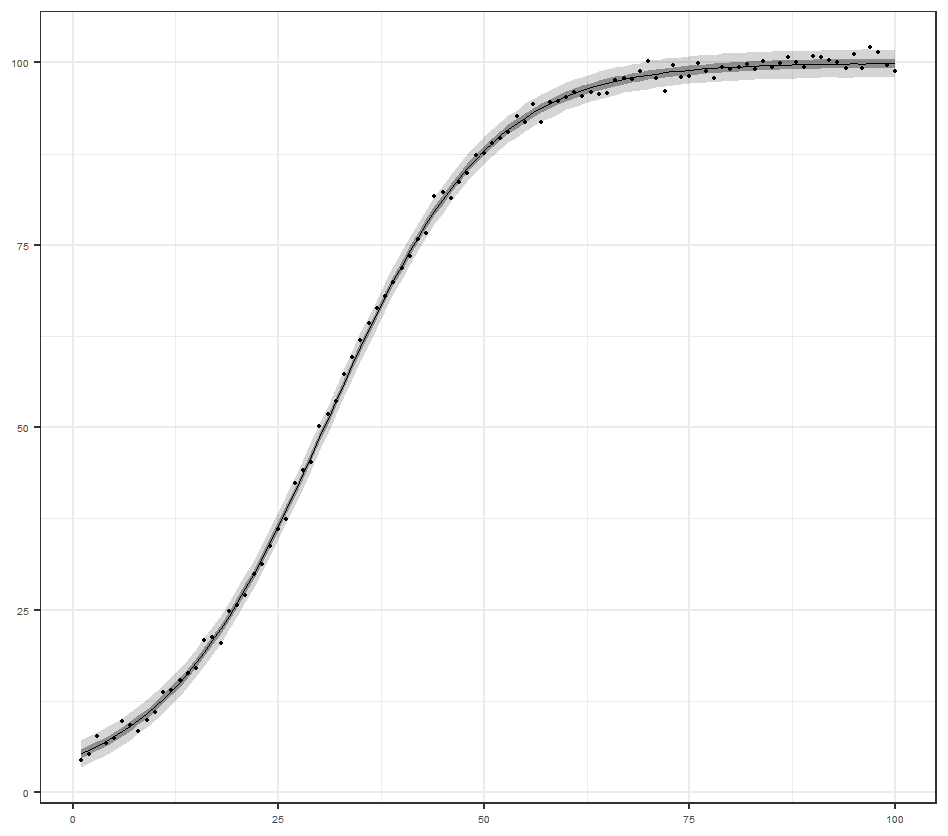
ポアソン分布のパラメータ$\lambda$の変化にともなう自由エネルギーの変化は次の通りです．

自由エネルギー（モデルにポアソン分布を仮定したとき）

このデータの平均の最尤推定値は2.84なので，自由エネルギーの定義上，$\lambda=2.84$のとき最小化します．

サンプルサイズ1000のデータセットを3000回発生させ，自由エネルギーを計算した結果を比較します．もはやRでは実行できないのでMathematicaに計算してもらいます．

Module[{xvec, out, out2},
 out = {samplesize = 1000, itr = 3000};
 Do[
  xvec = RandomVariate[NegativeBinomialDistribution[1, 0.25], 
    samplesize];
  out = Append[out, Fn[xvec, 1, 3]], {itr}
  ];
 out2 = {};
 Do[
  xvec = RandomVariate[NegativeBinomialDistribution[1, 0.25], 
    samplesize];
  out2 = Append[out2, Fnpois[xvec, Mean[xvec]]], {itr}
  ];
 Print[{Mean[out], Mean[out2]}];
 Histogram[{out, out2}]
 ]

自由エネルギーの分布の比較． オレンジは負の2項分布，青はポアソン分布

自由エネルギーの平均値は，

ポアソンモデル　2899.84　<　データを生成した分布（負の2項分布）　2910.24

でした．この条件でも平均自由エネルギーはデータを生成したモデルを選択しません．定義上，自由エネルギーの平均値は真のモデルと周辺尤度の交差エントロピーなので，周辺尤度を真の分布と一致するように作れば，自由エネルギーの平均も最小化するはずです．

式で書くと $$ \begin{align} E_{q(X^{n})}[F_n]&=-\int q(x^{n})\log p(x^{n}) dx^{n} \\ &=H[q(X^{n})]+D[q(X^{n})||p(X^{n})] \end{align} $$ なので，自由エネルギーの平均は真の分布のエントロピーと真の分布と周辺尤度のKL距離に分解できます．このうちKL距離は真の分布$q(X^{n})$と周辺尤度$p(X^{n})$ が一致しているのでゼロです．

しかし上記の条件では，データを発生させる真の分布とは異なる確率モデルのもとで，自由エネルギーがより小さな値をとっています．

なぜこうなるのか正直よく分かりません．原因が判明したら追記します．

*1:細かいことを言うと，ここでいう最尤推定モデルの自由エネルギーとは，事前分布が最尤推定値で質点を持つディラックデルタ分布であるようなベイズモデルの自由エネルギーと定義しておきます．これは実質的には最大対数尤度の－1倍と同じです

自由エネルギーの計算例1

イントロ

以前，Mathlogに自由エネルギーについて書きました．

mathlog.info

自由エネルギーは，データへのモデルのフィットを確認するために便利な指標の一つです． 特に，階層モデルでWAICの計算が煩雑な場合に，相対的に近似計算が簡単な自由エネルギーは重宝します． この指標を用いたモデル比較の意味について，単純例をつかって考えてみます．

意図

以下にいろいろと数値実験をやっていますが，知りたいことは 「データを生成する分布と一致するベイズモデルの自由エネルギー」と「データを生成する分布と一致しない最尤推定モデルの自由エネルギー」を比較するとどちらが小さいのか？ です．自由エネルギーの平均値は真のモデルと周辺尤度の交差エントロピーなので，周辺尤度を真の分布と一致するように作れば，自由エネルギーの平均もその場合に最小化する，と予想します．

それではさっそく計算してみましょう

実験1

まず，パラメータリカバリ用にベルヌーイ分布$\mathrm{Bernoulli}(0.2) $にしたがうデータを生成します． つまり真のパラメータは$q=0.2$です．

100個のデータを生成します．

x <- rbinom(100,1,0.2)

中身はこんな感じです．

> x
  [1] 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
 [43] 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0
 [85] 1 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0
> mean(x)
[1] 0.17

このデータを次の確率モデルと事前分布で学習します． $$ X \sim \mathrm{Bernoulli}(q) $$ $$ q \sim \mathrm{Beta}(a, b) $$ つまり，ベルヌーイ分布のパラメータ$q$の事前分布がベータ分布$\mathrm{Beta}(a, b)$にしたがう統計モデルです．

この統計モデルから自由エネルギーを計算してみましょう．

サンプルの実現値が$(x_1, x_2, ... , x_n)$であるとします．

このとき周辺尤度は $$ Z_n = \frac{B(\sum x_i+a,n-\sum x_i +b)}{B(a,b)} $$ です．ここで$B(a,b)$はベータ関数 $$ B(a,b)=\int_{0}^{1} x^{a-1}(1-x)^{b-1}dx $$ です．自由エネルギーは周辺尤度の対数符号反転ですから $$ F_n=-\log Z_n=-\log \frac{B(\sum x_i+a,n-\sum x_i +b)}{B(a,b)} $$ です．

これをそのままRで定義します．

Fn <- function(x,a,b){
-1*log(beta(sum(x)+a,length(x)-sum(x)+b)/beta(a,b))
}

この自由エネルギーに， さきほど生成したデータxを代入しつつ，事前分布のパラメータa,bを変化させて計算しましょう．

> Fn(x,a=2,b=8)
[1] 46.79755
> Fn(x,a=20,b=80)
[1] 46.05689
> Fn(x,a=200,b=800)
[1] 45.89823

自由エネルギーFn(x,a=2,b=8)は事前分布$\mathrm{Beta}(2, 8)$

自由エネルギーFn(x,a=20,b=80)は事前分布$\mathrm{Beta}(20, 80)$

自由エネルギーFn(x,a=200,b=800)は事前分布$\mathrm{Beta}(200, 800)$

にそれぞれ対応しています（確率モデルは全て共通で$\mathrm{Bernoulli}(q)$です）．ところでベータ分布の平均は$a/(a+b)$ですから $$ \frac{a}{a+b}=\frac{2}{2+8}=\frac{20}{20+80}=\frac{200}{200+800}=0.2 $$ となり，全ての事前分布の平均は，真のパラメータである$q=0.2$と一致しています．

またベータ分布の分散はパラメータの増加に対して減少するので，事前分布$\mathrm{Beta}(200, 800)$は 分散が小さいという意味で，この中では真のパラメータ$q=0.2$に，もっとも近い分布と言えるでしょう．

計算した自由エネルギーを比較すると，Fn(x,200,800)が最も小さな値を示しています．

ところで事前分布を $$ \mathrm{Beta}(200, 800), \mathrm{Beta}(2000, 8000), \mathrm{Beta}(20000, 80000), \mathrm{Beta}(200000, 800000), ...
$$ のょうに，パラメータの比率を一定のまま大きくしていくと，どうなるでしょうか．このベータ分布は， $q=0.2$で質点を持つようなディラックのデルタ分布に近づくことが分かります．

ここで$q=0.2$で質点を持つディラックのデルタ分布とは $$ \begin{align} d_{0.2} (q)=\begin{cases} 0 & (q\neq 0.2) \cr \infty & (q=0.2) \end{cases} \end{align} $$ と定義され $$ \int d_{0.2} ( q ) d q =1 \quad $$

$$ \int f ( q ) d_{0.2} ( q ) d q =f ( 0.2 ) $$ という性質を持つ超関数です．

では，所与のデータxのもとで，事前分布が$q=0.2$で質点を持つディラックのデルタ分布は自由エネルギーを最小化させることができるでしょうか？

そのことを確かめてみましょう．

データの平均は0.17だったので，平均位置が0.17であるようなベータ分布を事前分布として仮定します．

> Fn(x,a=1.7,b=8.3)
[1] 46.83316
> Fn(x,a=17,b=83)
[1] 45.93773
> Fn(x,a=170,b=830)
[1] 45.63632

自由エネルギーFn(x,a=1.7,b=8.3)は事前分布$\mathrm{Beta}(1.7, 8.3)$

自由エネルギーFn(x,a=17,b=83)は事前分布$\mathrm{Beta}(17, 83)$

自由エネルギーFn(x,a=170,b=830)は事前分布$\mathrm{Beta}(170, 830)$

にそれぞれ対応しています（確率モデルは全て共通で$\mathrm{Bernoulli}(q)$です）．

ここで事前分布の平均が0.2の場合の自由エネルギーFn(x,a=200,b=800)と事前分布の平均が0.17である場合の自由エネルギーFn(x,a=170,b=830)を比べてみると，

Fn(x,a=200,b=800) > Fn(x,a=170,b=830)

なので，真のパラメータに近い事前分布ではなく，データから得た平均値 に近い事前分布のほうが自由エネルギーが小さいことが分かります．なお，データの平均値はこの場合，ベルヌーイ分布からつくった尤度関数に基づく最尤推定値と一致します．

このように自由エネルギーによるモデル選択は，データを生成する真の分布を選ばないことがある，という点に注意してください．

ただしこの条件の下ではデータ数が増えれば，大数の法則によって最尤推定量が真のパラメータに確率収束するので，自由エネルギーを最小化する事前分布は真のパラメータ値を質点とするディラックのデルタ分布と一致します．

長くなったので続きます

GithubアカウントをSourcetree で認証させる方法

久しぶりにSourcetree（GitをGUI操作するためのローカルクライアント）を経由してGithub上のファイルを更新しようとしたら，「Githubの認証方式が変わったのでアクセスできません」というエラーが発生しました．

qiita.com

こちらを参考にトークンでの認証に切り替えたところ，うまくプッシュできるようになりました． なおトークンを発行しても，クライアントを介さずにGithubにログインする場合は，従来のパスワードでログインできています．

注意すべきは，SourcetreeのオプションでGithubアカウントを編集してパスワード部分を新たに発行したトークンに更新しても，それだけではうまくいかないところです．

上記の記事に書いてあるとおり，appdataに保存されているパスワードを削除する必要があります．なおappdataは「隠しファイルを表示」で中身を確認できます．

まだ設定してないマシンが残っているのですが，設定する頃にはやり方を忘れているはずなので，自分のためのメモでした．

ベイズ予測分布のplot

イントロ

この記事はベイズ予測分布を応答変数データのヒストグラムに重ねてplotする方法のメモです．

目的

応答変数が離散的なスケールで測定されている場合，bayesplotのppc_dens_overlay関数が使えなくて面倒くさいってことがあります．

無理矢理やると，こんな感じになり，泣けてきます．

ppc_dens_overlay

というわけで，離散的な応答変数に連続関数の予測分布を重ねる方法を考えました．

bayesplotの設定で対応できるのかもしれませんが，どうせ後で凡例などを修正したくなるはずなので，先を見越してggplotで自作します．

準備

まずStanの出力stanfitオブジェクトからパラメータの事後分布を取り出し， ベイズ予測分布をRで定義します．

fit <- extract(stanfit)
predict<-function(x) {
  mean(dnorm(x,fit$mu,fit$sigma)) #確率モデルにパラメータをベクトルで代入
}

確率モデルは正規分布を仮定しています．

ここでfit$mu, fit$sigmaの長さはMCMCサンプルの個数と一致します．たとえばチェイン3で反復1500，バーンインが500と仮定すれば MCMCサンプルの個数は$(1500-500)\times 3=3000$です．

関数predictは，確率モデルに事後分布の実現値（MCMCサンプル）を代入した値の平均なので，実質的には確率モデルの事後分布による平均（ベイズ予測モデル）の近似になっています（予測分布が解析的に出てくる場合はこの関数は必要ありません）．

次に予測分布predictを使って，pdfの値を計算します．

pdf<-map_dbl(seq(0.10,0.02),predict)

seqの範囲はpdfの長さがMCMCではなくデータのサンプルサイズに一致するように適当に調整します．

なぜかといえば，ggplotで応答変数のヒストグラムとpdfの曲線を重ねたいからです．

ggplotのコ－ドは例えば次のようなものになるでしょう．

d1 <- data.frame(Level=y,yp=pdf,xaxis=seq(0,10,0.02))
ggplot(d1,aes(x=Level,y=..density..)) + 
    geom_histogram(binwidth=1,fill="white",colour="black")+
    geom_line(aes(x=xaxis,y=pdf))

結果はたとえば次のとおりです．

ベイズ予測分布とデータのヒストグラム

テスト用にサンプルサイズを小さくしたので，あまりフィットしていませんが，まあいいでしょう．

説明変数があるとき

さていろいろ試しているうちに，説明変数がある場合の予測分布の定義がよく分からないことに気づきました． パラメータが説明変数によって変化するモデル，典型的には次のような線形回帰モデルです*1．

$$ Y_i \sim N( \beta_{0} +\beta_1 X_i, s^{2}) \quad i=1,2,...,n $$

予測分布の定義を次のように書き換えます．

predict<-function(y) {
    dnormlist <- c()
    for(i in 1:n){
    dnormlist <- append(dnormlist,dnorm(y,fit$b0+fit$b1*x1[i]))
    }
    mean(dnormlist)
}

ここでx1が説明変数です．サンプル$i$ごとに事後分布で確率モデルを平均し，さらに最後にサンプル方向に平均します．

テスト用に応答変数が説明変数によって二峰型になるパタンを考えてみましょう

n <- 150 # sample size
x1 <- c(rep(0,n/2),rep(5,n/2))#説明変数
y <-c()
for(i in 1:n){
    y <- append(y,rnorm(1,x1[i],1))
}  

予測分布を当てはめます．

ベイズ予測分布とデータのヒストグラム

多分もっと効率のよい書き方があると思いますので気づいたら直します．

*1:はてぶろではsigmaが使えない！なんてこった

微分方程式と状態空間モデル

イントロ

微分方程式をベースにした統計モデルに関して興味深い論文を読んだので紹介します．

Naik, Prasad A., Murali K. Mantrala and Alan G. Sawyer, 1998, Planning Media Schedules in the Presence of Dynamic Advertising Quality, Marketing Science, Vol. 17, No. 3, pp. 214-235

https://www.jstor.org/stable/193228

広告のタイミングと売上の関係を時系列データで分析するという内容です． この中で特に私が注目したのは以下の部分です．

In Table 2, we briefly describe the extant models we have chosen to compare with the proposed model, namely, the models of Vidale and Wolfe [ 1957 ] , Nerlove and Arrow [1962], Brandaid [ Little 1975 ], Tracker [ Blattberg and Golanty 1978 ], and Litmus [ Blackburn and Clancy 1982 ]. It is interesting to note that these five well-known models can be cast into the same state-space form that was employed to estimate the proposed model.

筆者らは，微分方程式をベースにした理論モデルが状態空間モデルで表現できる（埋め込むことができる）と述べています．

はじめはよく分からなかったのですが，彼らのアイデアを理解するにつれ，次第に「なるほど確かにこういう方法は有用かもしれない」と思い至りました．

Naik らのアイデア

論文内で参照している five well-known models はいずれも微分方程式モデルです．Naik らのアイデアの骨子は，微分方程式を陽表的に解くのではなく，離散化した微分方程式を状態空間モデルの状態方程式として使う，というものです．

たとえばVidal-Wolfeモデルは $$ \frac{ds}{dt}+\left( \frac{rA}{M} + \beta \right)s= rA $$ という微分方程式なので，これを陽表的に解くと，特殊解は $$ s=f(t) $$ という形で表すことができます（厳密には条件分岐しますがちょっと省略して書いてます）．したがってこの特殊解を決定論的パラメータとしてもつ観測誤差関数を定義すれば，カルマンフィルタでパラメータを推定したり，ベイズモデル化して予測分布を計算できます． 一方でNaikらの方法は離散化によって微分方程式を近似するため，わざわざ特殊解を特定する必要がありません．それゆえ計算がむずかしい微分方程式モデルに対して適用可能です． integrate_ode( )を使って微分方程式をstanに計算させることも可能ですが，簡単な条件下では「微分方程式＋状態空間モデル」のほうが手軽です. *1

パラメータリカバリ

Naikらのアイデアをパラメータリカバリで確認してみましょう． まず分析用のデータは次の微分方程式 $$ \frac{dy}{dt} = r y \frac{m - y}{m}, 　t=0　のとき　y=y_0 $$ から得た特殊解 $$ y= \frac{\exp\{ rt \}m y_0 } { m- y_0+ \exp\{ rt \} y_0} $$ に誤差を足した値であると定義します．

Rコードで書くとこんな感じです．

r <- 0.1  #増加率パラメータ　推定対象
m <- 100  # 上限
y0 <- 5  #初期値
n <- 100  #データ数．
sigma <- 1
for (t in 1:n) {
Y[t] <- rnorm(1, (exp(r*(t-1))*m*y0) / (m - y0 + exp(r*(t-1))*y0),sigma)
}

このデータを，つぎの三つの統計モデルで予測します．

1. 決定論的関数＋観測誤差モデル
2. ローカルレベルの状態空間モデル
3. 離散化した微分方程式を状態方程式とする状態空間モデル

それぞれのstanコードは以下の通りです．*2

まず決定論的関数＋観測誤差モデル

data {
  int n;//期間
  real Y[n];//観測値
  real y0data;//初期値
real m;
}

parameters {
  real<lower=0,upper=2> s_v;  // 観測誤差の標準偏差
  real<lower=0,upper=1>r;//増加パラメータ
}

model {
target += uniform_lpdf(s_v|0,2);
target += uniform_lpdf(r|0,1);
target += uniform_lpdf(mu|0,100);
for(i in 1:n) {
target += normal_lpdf(Y[i]|(exp(r*(i-1))*m*y0data) / (m - y0data + exp(r*(i-1))*y0data), s_v);
  }
}

generated quantities{
    real y_pred[n];
  for(i in 1:n){
    y_pred[i] = normal_rng((exp(r*(i-1))*m*y0data) / (m - y0data + exp(r*(i-1))*y0data), s_v);}
}

次にローカルレベルの状態空間モデル

data {
  int n;//期間
  real Y[n];//観測値
}

parameters {
  real<lower=0,upper=2> s_w;  // 過程誤差の標準偏差
  real<lower=0,upper=2> s_v;  // 観測誤差の標準偏差
  real<lower=0,upper=100> mu[n];// 状態の推定値(水準成分)
}

model {
target += uniform_lpdf(s_w|0,2);
target += uniform_lpdf(s_v|0,2);
for(i in 2:n) {
target += normal_lpdf(mu[i]|mu[i-1], s_w);//いわゆるローカルレベルモデル
  }
for(i in 1:n) {
target += normal_lpdf(Y[i]|mu[i], s_v);
  }
}

generated quantities{
    real y_pred[n];
  for(i in 1:n){
    y_pred[i] = normal_rng(mu[i], s_v);}
}

最後に微分方程式を状態方程式とする状態空間モデル

data {
  int n;//期間
  real Y[n];//観測値
  real m;//上限
}

parameters {
  real<lower=0,upper=2> s_w;  // 過程誤差の標準偏差
  real<lower=0,upper=2> s_v;  // 観測誤差の標準偏差
  real mu[n];// 状態の推定値(水準成分)
  real<lower=0,upper=1>r;//増加パラメータ
}

model {
target += uniform_lpdf(s_w|0,2);
target += uniform_lpdf(s_v|0,2);
target += uniform_lpdf(r|0,1);
for(i in 2:n) {
target += normal_lpdf(mu[i]|mu[i-1]+r*mu[i-1]*((m-mu[i-1])/m), s_w);
//状態方程式を微分方程式（ロジスティック）で代替する
  }
for(i in 1:n) {
target += normal_lpdf(Y[i]|mu[i], s_v);
  }
}

generated quantities{
    real y_pred[n];
  for(i in 1:n){
    y_pred[i] = normal_rng(mu[i], s_v);}
}

結果を比較します．

微分方程式の特殊解＋誤差モデル

微分方程式特殊解＋誤差

この統計モデルはデータを生成した真の分布と一致しているので，まあ当然の結果と言えるでしょう．

ローカルレベル状態空間モデル

ローカルレベル状態空間モデル

これは1期前の状態+システム誤差で現在の状態が決まるモデルです．

離散化した微分方程式を状態方程式とする状態空間モデル

離散化した微分方程式を状態方程式とする状態空間モデル

今回実験してみたかったモデルです．いい感じにフィットしているようです．

各統計モデルの自由エネルギーを計算したデータへのフィットを確認します．

1. 微分方程式の特殊解＋誤差モデル　143.1769
2. ローカルレベル状態空間モデル　228.1158
3. 微分方程式を状態方程式とする状態空間モデル　148.0088

特殊解を使った正解のモデルと，微分方程式＋状態空間モデルで近似したモデルの自由エネルギーはほぼ等しい値でした．

時間以外の説明変数があるデータのほうが，Naikらのアイデアは真価を発揮するのではないかと予想します．

*1:ただし連立微分方程式は integrate_ode( ) でないと無理かもしれません

*2:状態空間モデルのtarget記法はもしかしたら間違っているかもしれません．ここが間違っていれば自由エネルギーの計算結果が少し変わります．予測分布の計算には支障がないはずです．

ケースファンの回転数調整

PCがうるさい

なんだかPCがうるさい．HWMonitorで確認したらケースファンの回転数が常時1000RPMを超えていました．

マザーボードの設定を変えたら静かになったのですが，多分3日後にはやり方を忘れてしまうので記録を残しておきます．

4ピンではなく3ピンのコネクタだった

ケースを開けて，ケースファンのコネクタを外してみると4ピンではなく3ピンでした． 3ピンの場合は確か電圧で回転数を変更できるはずなので，BIOSもといマザボのUEFIを起動します． これはMSI社製のマザボの設定画面です．起動時にdelキーを押すとこの画面が出てきます（メーカーによってこのキーがF2だったりします）．

Fan Infoから当該ケースファンに対応しているものを選択してください．

マザボの設定

ファン制御の設定を見ると，PWMになっています．PWMで制御できない3ピンコネクタを挿しているせいでしょうか，回転数が1000RPMを超えています．どうやらここが騒音の元凶のようです．

PWMからDCに変更します．340RPMに下がり，かなり静かになりました．主観的幸福感が0.5ポイントほど上昇しました．ちなみにこのマザボのUEFIは，温度別に回転数を細かく設定できます．この設定ができないマザボの場合，AutoとかSilentなどのモードを選ぶとよいでしょう．

メーカーによって多少違いはありますが，設定は似ているはずなので，ファンがうるさいなと思ったら試してみてください（ただし回転数を下げるとケース内温度は上がるので，その辺は適度に調整してください）．

CPUファン

このマザボで使用しているCPUファンはサイドフロー型（横方向にファンを2個つけて風を前から後ろに流すタイプ）なのですが，ケース後方側のファンの取り付け方向が間違っていました．これをついでに直したおかげで，静かになったうえに温度も下がりました（オイ）．

オブジェクトやファイル名をループ内で割り当てる（R）

ファイル名を直書きするのがめんどうくさい

50個のデータセットを使い複数のモデルで推定して自由エネルギーを計算する必要があったのでコードを書いてみました．

多分忘れるだろうから，ここに貼り付けておきます．

fevalues.m0 <- c()
for (i in 1:50) {
  stanfit <-stan(file='model0.stan',iter=10500,warmup=500,data=f2(i),chains=4)
  saveRDS(stanfit,c(paste('fit/fe', i,'_0.rds', sep = '')))
  fevalues.m0 <- append(fevalues.m0,-logml(bridge_sampler(stanfit,method="warp3"))
  )
}  

ここで関数f2( )はstan用に各データセットをlist型に整形する関数です． stan( )の引数dataに関数の出力を渡しても問題ないようです．

途中でRがコケてもstanfitが残るようにsaveRDSで逐次保存します．このときpaste( )をforループで回してデータセットに対応したファイル名を自動作成します（10個くらいなら直打ちのほうが早いでしょう．50×3個のファイル名はさすがに書く気がしない）． saveRDS内でpaste( )を使っても問題ないようです．

stanfitは上書きされて1つしか残らないため，メモリ不足でRがクラッシュすることを防ぎます（多分）

計算した統計量（ここではブリッジサンプリングから計算した自由エネルギー）は空のベクトルfevalues.m0にappendしていきます．

モデルを変える場合は，stan( )のモデル部分だけ変え，上記のfor文をコピペして使い回します． 1回のループにまとめることもできますが，かえって可読性が悪くなると判断しました． このくらいで分割した方が，数ヶ月後の自分には理解しやすいでしょう．

呼び出したstanfitからの計算

readRDSで保存したstanfitを使ってbridge_sampler( )を適用すると，「modelがないぞ」とrstanに怒られます．

「コンパイルしたモデルは保存する設定にしとるやろがい！」と悪態をつきたくなる気持ちをぐっとこらえ，stanfitに対応したモデルをchains=0で再コンパイルします（これは時間はかかりません）．

mod<-stan(file='model0.stan',iter=10500,warmup=500,data=f2(i),chains=0)
-logml(bridge_sampler(stanfit,mod,method="warp3"))

これなら計算してくれます．

他に解決策があるのかもしれませんが，今回はこれでOKとします．