イントロ
微分方程式をベースにした統計モデルに関して興味深い論文を読んだので紹介します.
Naik, Prasad A., Murali K. Mantrala and Alan G. Sawyer, 1998, Planning Media Schedules in the Presence of Dynamic Advertising Quality, Marketing Science, Vol. 17, No. 3, pp. 214-235
https://www.jstor.org/stable/193228
広告のタイミングと売上の関係を時系列データで分析するという内容です. この中で特に私が注目したのは以下の部分です.
In Table 2, we briefly describe the extant models we have chosen to compare with the proposed model, namely, the models of Vidale and Wolfe [ 1957 ] , Nerlove and Arrow [1962], Brandaid [ Little 1975 ], Tracker [ Blattberg and Golanty 1978 ], and Litmus [ Blackburn and Clancy 1982 ]. It is interesting to note that these five well-known models can be cast into the same state-space form that was employed to estimate the proposed model.
筆者らは,微分方程式をベースにした理論モデルが状態空間モデルで表現できる(埋め込むことができる)と述べています.
はじめはよく分からなかったのですが,彼らのアイデアを理解するにつれ,次第に「なるほど確かにこういう方法は有用かもしれない」と思い至りました.
Naik らのアイデア
論文内で参照している five well-known models はいずれも微分方程式モデルです.Naik らのアイデアの骨子は,微分方程式を陽表的に解くのではなく,離散化した微分方程式を状態空間モデルの状態方程式として使う,というものです.
たとえばVidal-Wolfeモデルは
$$
\frac{ds}{dt}+\left( \frac{rA}{M} + \beta \right)s= rA
$$
という微分方程式なので,これを陽表的に解くと,特殊解は
$$
s=f(t)
$$
という形で表すことができます(厳密には条件分岐しますがちょっと省略して書いてます).したがってこの特殊解を決定論的パラメータとしてもつ観測誤差関数を定義すれば,カルマンフィルタでパラメータを推定したり,ベイズモデル化して予測分布を計算できます.
一方でNaikらの方法は離散化によって微分方程式を近似するため,わざわざ特殊解を特定する必要がありません.それゆえ計算がむずかしい微分方程式モデルに対して適用可能です.
integrate_ode( )を使って微分方程式をstanに計算させることも可能ですが,簡単な条件下では「微分方程式+状態空間モデル」のほうが手軽です.
*1
パラメータリカバリ
Naikらのアイデアをパラメータリカバリで確認してみましょう. まず分析用のデータは次の微分方程式 $$ \frac{dy}{dt} = r y \frac{m - y}{m}, t=0 のとき y=y_0 $$ から得た特殊解 $$ y= \frac{\exp\{ rt \}m y_0 } { m- y_0+ \exp\{ rt \} y_0} $$ に誤差を足した値であると定義します.
Rコードで書くとこんな感じです.
r <- 0.1 #増加率パラメータ 推定対象 m <- 100 # 上限 y0 <- 5 #初期値 n <- 100 #データ数. sigma <- 1 for (t in 1:n) { Y[t] <- rnorm(1, (exp(r*(t-1))*m*y0) / (m - y0 + exp(r*(t-1))*y0),sigma) }
このデータを,つぎの三つの統計モデルで予測します.
それぞれのstanコードは以下の通りです.*2
まず決定論的関数+観測誤差モデル
data { int n;//期間 real Y[n];//観測値 real y0data;//初期値 real m; } parameters { real<lower=0,upper=2> s_v; // 観測誤差の標準偏差 real<lower=0,upper=1>r;//増加パラメータ } model { target += uniform_lpdf(s_v|0,2); target += uniform_lpdf(r|0,1); target += uniform_lpdf(mu|0,100); for(i in 1:n) { target += normal_lpdf(Y[i]|(exp(r*(i-1))*m*y0data) / (m - y0data + exp(r*(i-1))*y0data), s_v); } } generated quantities{ real y_pred[n]; for(i in 1:n){ y_pred[i] = normal_rng((exp(r*(i-1))*m*y0data) / (m - y0data + exp(r*(i-1))*y0data), s_v);} }
次にローカルレベルの状態空間モデル
data { int n;//期間 real Y[n];//観測値 } parameters { real<lower=0,upper=2> s_w; // 過程誤差の標準偏差 real<lower=0,upper=2> s_v; // 観測誤差の標準偏差 real<lower=0,upper=100> mu[n];// 状態の推定値(水準成分) } model { target += uniform_lpdf(s_w|0,2); target += uniform_lpdf(s_v|0,2); for(i in 2:n) { target += normal_lpdf(mu[i]|mu[i-1], s_w);//いわゆるローカルレベルモデル } for(i in 1:n) { target += normal_lpdf(Y[i]|mu[i], s_v); } } generated quantities{ real y_pred[n]; for(i in 1:n){ y_pred[i] = normal_rng(mu[i], s_v);} }
data { int n;//期間 real Y[n];//観測値 real m;//上限 } parameters { real<lower=0,upper=2> s_w; // 過程誤差の標準偏差 real<lower=0,upper=2> s_v; // 観測誤差の標準偏差 real mu[n];// 状態の推定値(水準成分) real<lower=0,upper=1>r;//増加パラメータ } model { target += uniform_lpdf(s_w|0,2); target += uniform_lpdf(s_v|0,2); target += uniform_lpdf(r|0,1); for(i in 2:n) { target += normal_lpdf(mu[i]|mu[i-1]+r*mu[i-1]*((m-mu[i-1])/m), s_w); //状態方程式を微分方程式(ロジスティック)で代替する } for(i in 1:n) { target += normal_lpdf(Y[i]|mu[i], s_v); } } generated quantities{ real y_pred[n]; for(i in 1:n){ y_pred[i] = normal_rng(mu[i], s_v);} }
結果を比較します.
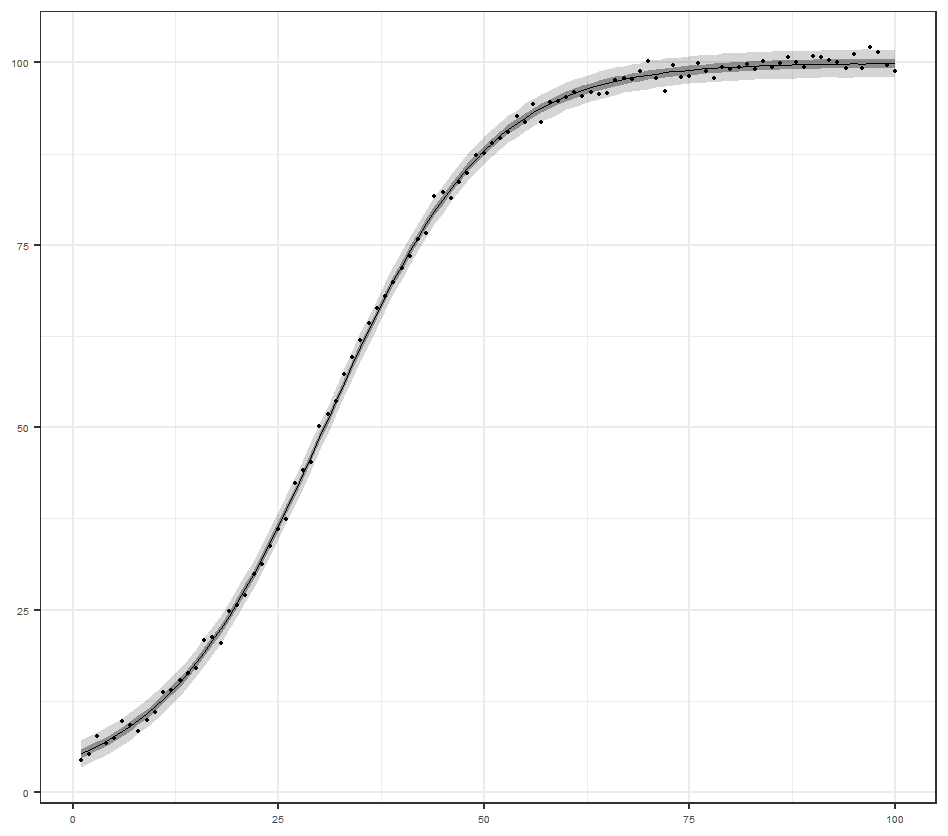
微分方程式の特殊解+誤差モデル

この統計モデルはデータを生成した真の分布と一致しているので,まあ当然の結果と言えるでしょう.
ローカルレベル状態空間モデル
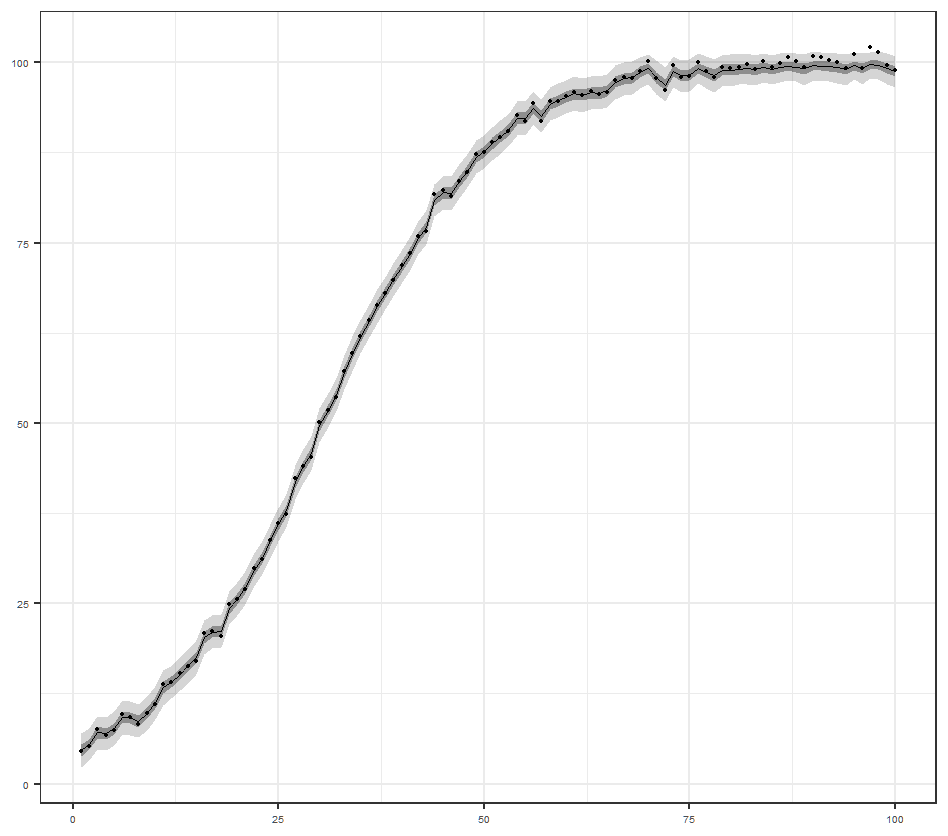
これは1期前の状態+システム誤差で現在の状態が決まるモデルです.
離散化した微分方程式を状態方程式とする状態空間モデル
今回実験してみたかったモデルです.いい感じにフィットしているようです.
各統計モデルの自由エネルギーを計算したデータへのフィットを確認します.
特殊解を使った正解のモデルと,微分方程式+状態空間モデルで近似したモデルの自由エネルギーはほぼ等しい値でした.
時間以外の説明変数があるデータのほうが,Naikらのアイデアは真価を発揮するのではないかと予想します.